Packages

We require the package surveillance (which you’ve already installed for the first part of the tutorial). Some bonus parts require the hhh4addon package, which can be installed directly from GitHub using the remotes package (see below).

library(surveillance)
Lade nötiges Paket: sp
Lade nötiges Paket: xtable
This is surveillance 1.23.1; see 'package?surveillance' or
https://surveillance.R-Forge.R-project.org/ for an overview.

Example data

We will use data from routine surveillance in Germany carried out by Robert Koch Institute. We have already prepared the data as "sts", so you can directly load them from an RData file.

load("data/data_BE.RData", verbose = TRUE)
Loading objects:
  noroBE
  rotaBE

We focus on the noroBE data, which contain weekly counts confirmed of norovirus cases in Berlin, 2011–2017. There is also rotaBE, which contains the same for rotavirus and which you may use in case you want to play around a bit more.

Exploring the data

Start by exploring the temporal and spatial distribution of the data. You can find different plotting options in ?plot.sts.

Solution 
# look at data:
# time series:
plot(noroBE, ylim = c(0, 40))

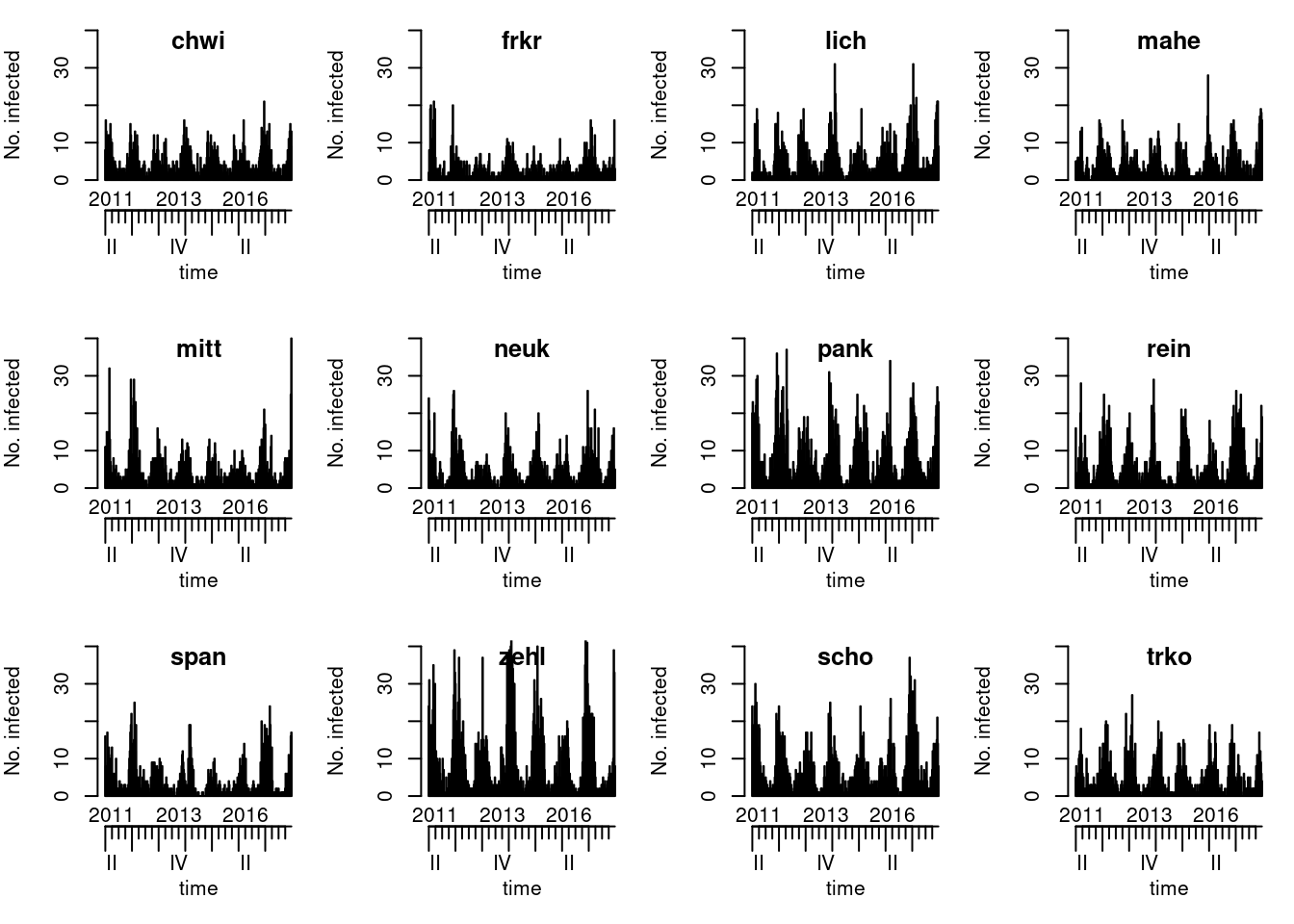
# map:
# as population(noroBE) contains population fractions rather than raw
# population sizes setting population = 100000/<population of Berlin>
# will yield cumulative incidence per 100.000 inhabitants; see ?stsplot_space
plot(noroBE, observed ~ unit, population = 100000/3500000, labels = TRUE)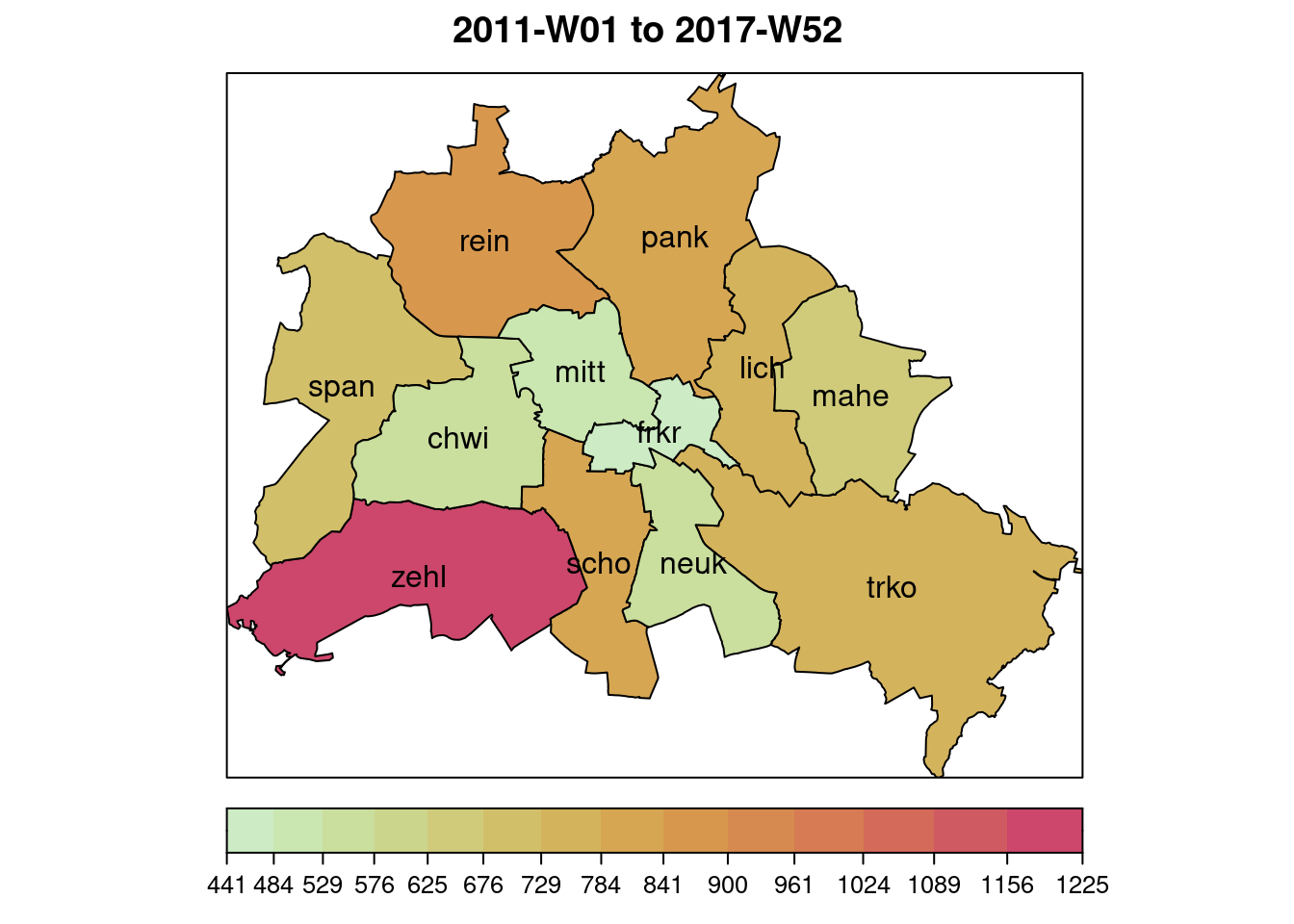

We moreover take a look at the slots populationFrac (population fraction) and neighbourhood of the sts object. The latter contains path distances between the districts: e.g., chwi and frkr have a distance of 2 as you need to go through mitt or scho. These distances will later be relevant for spatial coupling.

Give me a hint on where to find these You can list the contents of an sts object using str(). Note that as we are dealing with an S4 object, it has slots, which can be accessed using @ rather than $.
Solution 
# population:
head(noroBE@populationFrac)
          chwi       frkr      lich       mahe       mitt       neuk      pank       rein
[1,] 0.0923389 0.07839664 0.0755159 0.07226963 0.09709093 0.09083884 0.1073534 0.06971871
[2,] 0.0923389 0.07839664 0.0755159 0.07226963 0.09709093 0.09083884 0.1073534 0.06971871
[3,] 0.0923389 0.07839664 0.0755159 0.07226963 0.09709093 0.09083884 0.1073534 0.06971871
[4,] 0.0923389 0.07839664 0.0755159 0.07226963 0.09709093 0.09083884 0.1073534 0.06971871
[5,] 0.0923389 0.07839664 0.0755159 0.07226963 0.09709093 0.09083884 0.1073534 0.06971871
[6,] 0.0923389 0.07839664 0.0755159 0.07226963 0.09709093 0.09083884 0.1073534 0.06971871
           span       zehl       scho      trko
[1,] 0.06537046 0.08505422 0.09617513 0.0698772
[2,] 0.06537046 0.08505422 0.09617513 0.0698772
[3,] 0.06537046 0.08505422 0.09617513 0.0698772
[4,] 0.06537046 0.08505422 0.09617513 0.0698772
[5,] 0.06537046 0.08505422 0.09617513 0.0698772
[6,] 0.06537046 0.08505422 0.09617513 0.0698772
# note: this is a matrix as in principle the population faction could vary over time.
# neighbourhood structure:
noroBE@neighbourhood # neighbourhood(noroBE) does the same
     chwi frkr lich mahe mitt neuk pank rein span zehl scho trko
chwi    0    2    3    4    1    2    2    1    1    1    1    3
frkr    2    0    1    2    1    1    1    2    3    2    1    1
lich    3    1    0    1    2    2    1    2    3    3    2    1
mahe    4    2    1    0    3    2    2    3    4    4    3    1
mitt    1    1    2    3    0    2    1    1    2    2    1    2
neuk    2    1    2    2    2    0    2    3    3    2    1    1
pank    2    1    1    2    1    2    0    1    2    3    2    2
rein    1    2    2    3    1    3    1    0    1    2    2    3
span    1    3    3    4    2    3    2    1    0    1    2    4
zehl    1    2    3    4    2    2    3    2    1    0    1    3
scho    1    1    2    3    1    1    2    2    2    1    0    2
trko    3    1    1    1    2    1    2    3    4    3    2    0

Developing a multivariate model step by step

Step 1: Seasonality in the endemic component, all parameters shared, no coupling.

We start by a very simple model where for districts \(i = 1, \dots, K\) we assume \[\begin{align} Y_{it} \ \mid \ \ \text{past} & \sim \text{NegBin}(\mu_{it}, \psi)\\ \mu_{it} & = \nu_t + \lambda Y_{i, t - 1} \end{align}\] and \[ \nu_{t} = \alpha^\nu + \beta^\nu \sin(2\pi t/52) + \gamma^\nu \cos(2\pi t/52). \] This model features neither region-speciic parameters nor spatial coupling. To get you started the code for this model is provided. In the following steps you’ll be able to extend upon this basic formulation.

Click for an intuitive visual sketch of this model

In a setting with just \(K = 3\) districts the model could be illustrated as follows – case numbers the different districts are independent and only depend on the previous value in the same district.

Code:

# first define a subset of the data to which to fit (will be used in all model
# fits to ensure comparability of AIC values):
subset_fit <- 6:(nrow(noroBE@observed) - 52)
# we are leaving out the last year and the first 5 observations
# the latter serves to ensure comparability models with 
# higher-order lags, see below.

##################################################################
# Model 1:
# control list:
ctrl1 <- list(end = list(f = addSeason2formula(~1, S = 1)), # seasonality in end
              # S = 1 means one pair of sine / cosine waves is included
              ar = list(f = ~ 1), # no seasonality in ar
              family = "NegBin1", # negative binomial (rather than Poisson)
              subset = subset_fit)
# fit model
fit1 <- hhh4(noroBE, ctrl1)

To inspect the model fit you can check out its summary and some plots (check ?plot.hhh4 for options).

Solution 
# summary of parameter estimates:
summary(fit1)

Call: 
hhh4(stsObj = noroBE, control = ctrl1)

Coefficients:
                        Estimate  Std. Error
ar.1                    -0.72854   0.03453  
end.1                    0.84477   0.02860  
end.sin(2 * pi * t/52)   0.09024   0.02806  
end.cos(2 * pi * t/52)   0.88574   0.02856  
overdisp                 0.22957   0.01076  

Log-likelihood:   -8780.82 
AIC:              17571.64 
BIC:              17602.7 

Number of units:        12 
Number of time points:  307 
# you can set idx2Exp = TRUE to get all estimates on the exp-transformed scale
summary(fit1, idx2Exp = TRUE)

Call: 
hhh4(stsObj = noroBE, control = ctrl1)

Coefficients:
                             Estimate  Std. Error
exp(ar.1)                    0.48261   0.01667   
exp(end.1)                   2.32745   0.06657   
exp(end.sin(2 * pi * t/52))  1.09443   0.03071   
exp(end.cos(2 * pi * t/52))  2.42477   0.06925   
overdisp                     0.22957   0.01076   

Log-likelihood:   -8780.82 
AIC:              17571.64 
BIC:              17602.7 

Number of units:        12 
Number of time points:  307 
# visually inspect:
plot(fit1, unit = 1:12) # look at all units

# get AIC to compare model fit to more complex models
AIC(fit1)
[1] 17571.64

For model inspection I like looking at Pearson residuals \[ \frac{Y_{it} - \hat{\mu}_{it}}{\hat{\sigma}_{it}} = \frac{Y_{it} - \hat{\mu}_{it}}{\sqrt{\hat{\mu}_{it} + \hat{\mu}_{it}^2/\psi}}. \] In a well-specified model, the Pearson residuals should have roughly mean 0, standard deviation 1 and no autocorrelation.

residuals() with type = "pearson" are currently only available in the
development version of surveillance (not needed)

which you might be able to install via (untested)

## install.packages("surveillance", repos = c("https://r-forge.r-universe.dev", "https://cloud.r-project.org"))

but you can instead use the following little auxiliary function:

# helper function to compute Pearson residuals. Just provide the model fit 
# as the only argument.
# returns a matrix with Pearson residuals in the different strata (columns)
# and time points (rows)
# note: this is a bit more complicated as it also handles an extended version
# of the hhh4 class called hhh4lag
pearson_residuals <- function(hhh4Obj){
  # compute raw residuals:
  response_residuals <- residuals(hhh4Obj, type = "response")
  # compute standard deviations:
  if(inherits(hhh4Obj, "hhh4lag")){
    sds <- sqrt(fitted(hhh4Obj) + 
                  fitted(hhh4Obj)^2/hhh4addon:::psi2size.hhh4lag(hhh4Obj))
  }else{
    sds <- sqrt(fitted(hhh4Obj) + 
                  fitted(hhh4Obj)^2/surveillance:::psi2size.hhh4(hhh4Obj))
  }
  # compute Pearson residuals:
  pearson_residuals <- response_residuals/sds
  return(pearson_residuals)
}

On a side note: surveillancedoes support deviance residuals, which serve a similar purpose, see ?residuals.hhh4.

Compute some region-wise summary statistics of Pearson residuals to get an idea of the shortcomings of this model.

Solution 
pr1 <- pearson_residuals(fit1)
# deviance residuals as implemented in the package
# serve a similar purpose and are quite similar
# for large count values.
# dr1 <- residuals(fit1, type = "deviance")


# compute district-wise means and standard deviations:
colMeans(pr1)
        chwi         frkr         lich         mahe         mitt         neuk         pank 
-0.040128818 -0.354497174 -0.026596771 -0.149654100 -0.098957012 -0.139634691  0.363677331 
        rein         span         zehl         scho         trko 
-0.006394507 -0.203281407  0.422776136  0.208763434 -0.023204469 
apply(pr1, 2, sd)
     chwi      frkr      lich      mahe      mitt      neuk      pank      rein      span 
0.8969573 0.8394516 0.9984702 0.9348625 0.9594755 0.8998828 1.1386447 0.9955265 0.9606598 
     zehl      scho      trko 
1.2538557 1.0589218 0.9730101 
# compute the ACF for a few strata
par(mfrow = c(1, 3))
acf(pr1[, 1])
acf(pr1[, 2])
acf(pr1[, 3])

In each district, the Pearson residuals should have mean and standard deviations of approximately 0 and 1, respectively, which is clearly not the case. By sharing all parameters, fitted values are systematically larger than observed in some districts and smaller in others.

Moreover, in a correctly specified model, the Pearson residuals would be uncorrelated, which is clearly not the case either.

Step 2: Adding district-specific parameters.

As the districts are of different sizes and have different incidence levels, we include district-specific parameters and extend the model to \[\begin{align} Y_{it} \ \mid \ \ \text{past} & \sim \text{NegBin}(\mu_{it}, \psi)\\ \mu_{it} & = \nu_{it} + \lambda_i Y_{i, t - 1}\\ \nu_{it} & = \alpha^\nu_i + \beta^\nu \sin(2\pi t/52) + \gamma^\nu \cos(2\pi t/52) \end{align}\] Note that the parameters for seasonality are still shared (though you can try out district-specific ones).

Try to fit this model to the data. You can check out ?fe on district-specific parameters.

Solution 
##################################################################
# Model 2:
# We use fe(..., unitSpecific = TRUE) to add fixed effects for each unit,
# in this case intercepts (1). Seasonality parameters are still shared
# across districts
ctrl2 <- list(end = list(f = addSeason2formula(~0 + fe(1, unitSpecific = TRUE),
                                               S = 1)),
              ar = list(f = ~ 0 + fe(1, unitSpecific = TRUE)),
              family = "NegBin1",
              subset = subset_fit)
# Note: ~0 is necessary as otherwise one would (implicitly) add two intercepts
# unit-specific dispersion parameters could be added by setting family = "NegBinM"
fit2 <- hhh4(noroBE, ctrl2)
# check parameter estimates:
summary(fit2)

Call: 
hhh4(stsObj = noroBE, control = ctrl2)

Coefficients:
                        Estimate   Std. Error
ar.1.chwi               -1.795086   0.402460 
ar.1.frkr               -1.259748   0.182296 
ar.1.lich               -1.087080   0.177651 
ar.1.mahe               -0.957952   0.145501 
ar.1.mitt               -1.335034   0.214060 
ar.1.neuk               -0.967629   0.159855 
ar.1.pank               -0.753360   0.129017 
ar.1.rein               -0.668191   0.103620 
ar.1.span               -0.823339   0.125950 
ar.1.zehl               -0.659794   0.095464 
ar.1.scho               -0.865145   0.132413 
ar.1.trko               -1.002428   0.165175 
end.sin(2 * pi * t/52)   0.121489   0.024384 
end.cos(2 * pi * t/52)   0.923900   0.024745 
end.1.chwi               1.181472   0.088438 
end.1.frkr               0.604251   0.081671 
end.1.lich               1.020524   0.089385 
end.1.mahe               0.791906   0.089509 
end.1.mitt               1.010631   0.081603 
end.1.neuk               0.823126   0.097049 
end.1.pank               1.298509   0.104632 
end.1.rein               0.791816   0.097056 
end.1.span               0.648208   0.092789 
end.1.zehl               1.297808   0.091415 
end.1.scho               1.189950   0.093128 
end.1.trko               0.997664   0.094204 
overdisp                 0.197678   0.009884 

Log-likelihood:   -8655.46 
AIC:              17364.92 
BIC:              17532.63 

Number of units:        12 
Number of time points:  307 
# compute AIC
AIC(fit2)
[1] 17364.92

Next, let’s again again check the Pearson residuals.

Solution 
# compute Pearson residuals and check their mean and variance:
pr2 <- pearson_residuals(fit2)
colMeans(pr2)
        chwi         frkr         lich         mahe         mitt         neuk         pank 
 0.020061368  0.025144794 -0.010413219  0.003481020 -0.004801394 -0.006139166 -0.012998766 
        rein         span         zehl         scho         trko 
-0.004079849 -0.001710578 -0.022435249 -0.007614639 -0.016314666 
apply(pr1, 2, sd)
     chwi      frkr      lich      mahe      mitt      neuk      pank      rein      span 
0.8969573 0.8394516 0.9984702 0.9348625 0.9594755 0.8998828 1.1386447 0.9955265 0.9606598 
     zehl      scho      trko 
1.2538557 1.0589218 0.9730101 
## These now look reasonable in terms of mean and standard deviations.

Note that we could also add district-specific dispersion parameters \(\psi_i\) by setting family = "NegBinM", but for simplicity we stick with the shared overdispersion parameter.

Step 3: Adding dependence between districts.

For now we have been modelling each district separately (while sharing some parameters). We now add dependencies via the ne (neighbourhood) component. The simplest version is a model where only direct neighbours affect each other, \[\begin{align} Y_{it} \ \mid \ \ \text{past} & \sim \text{NegBin}(\mu_{it}, \psi)\\ \mu_{it} & = \nu_{it} + \lambda_i Y_{i, t - 1} + \phi_i \sum_{j \sim i} w_{ji} Y_{j, t - 1}. \end{align}\] Here, the relationship \(\sim\) indicates direct neighbourhood. The weights \(w_{ji}\) can be chosen in two ways.

  • if normalize == TRUE: \(w_{ji} = 1/\) (number of neighbours of \(j\)) if \(i \sim j\), 0 else
  • if normalize == FALSE: \(w_{ji} = 1\) if \(i \sim j\), 0 else

We usually use normalize = TRUE, which is based on the intuition that each district splits up its infectious pressure equally among its neighbours. Note that in this formulation, the autoregression on past incidence from the same district and others are handled each on their own with separate parameters.

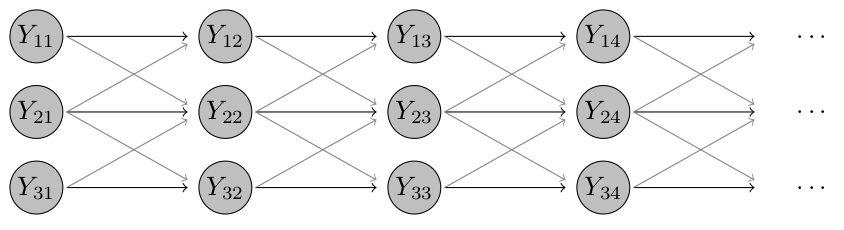
Click for an intuitive visual sketch of this model

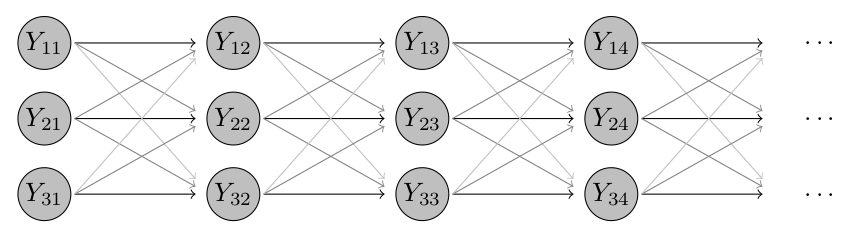
In our example with just three districts, where district 2 is neighbouring both 1 and 3, but 1 and 3 are not neighbours, the model looks as follows. The grey lines indicate that these dependencies are typically weaker than the ones to previous values from the same district.

As documented in ?hhh4, the neighbourhood weights \(w_{ji}\) are obtained from the matrix noroBE@nighborhood via noroBE@neighbourhood == 1. You can convince yourself up here that in the encoding used for the path distances, 1 indeed indicates direct neighbourhood. All other entries will be treated equally as “non-neighbours”.

Try to add an ne component to your model by modifying the control list or by using update. You can check out ?hhh4 for details.

Solution 
# The default setting for the ne component is to use weights 
# neighbourhood(stsObj) == 1 (see ?hhh4).
neighbourhood(noroBE) == 1
      chwi  frkr  lich  mahe  mitt  neuk  pank  rein  span  zehl  scho  trko
chwi FALSE FALSE FALSE FALSE  TRUE FALSE FALSE  TRUE  TRUE  TRUE  TRUE FALSE
frkr FALSE FALSE  TRUE FALSE  TRUE  TRUE  TRUE FALSE FALSE FALSE  TRUE  TRUE
lich FALSE  TRUE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE
mahe FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE
mitt  TRUE  TRUE FALSE FALSE FALSE FALSE  TRUE  TRUE FALSE FALSE  TRUE FALSE
neuk FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE  TRUE
pank FALSE  TRUE  TRUE FALSE  TRUE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE
rein  TRUE FALSE FALSE FALSE  TRUE FALSE  TRUE FALSE  TRUE FALSE FALSE FALSE
span  TRUE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE  TRUE FALSE FALSE
zehl  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE  TRUE FALSE
scho  TRUE  TRUE FALSE FALSE  TRUE  TRUE FALSE FALSE FALSE  TRUE FALSE FALSE
trko FALSE  TRUE  TRUE  TRUE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE
# this is because historically neighbourhood matrices were just binary
# however, the path distances are coded in a way that direct neighbours have 
# distance 1, meaning that there is no need to modify the neighbourhood matrix

##################################################################
# Model 3:
ctrl3 <- list(end = list(f = addSeason2formula(~0 + fe(1, unitSpecific = TRUE),
                                               S = 1)),
              ar = list(f = ~ 0 + fe(1, unitSpecific = TRUE)),
              ne = list(f = ~ 0 + fe(1, unitSpecific = TRUE), normalize = TRUE), 
              #  now added ne component to reflect cross-district dependencies
              family = "NegBin1",
              subset = subset_fit)
# normalize = TRUE normalizes weights by the number of neighbours of the 
# exporting district
fit3 <- hhh4(noroBE, ctrl3)
AIC(fit3)
[1] 17271.12
# alternative: use update
# fit3 <- update(fit2, ne = list(f = ~ 0 + fe(1, unitSpecific = TRUE),
#                                weights = neighbourhood(noroBE) == 1,  # little bug?
#                                normalize = TRUE))
summary(fit3) # parameters for different districts are quite different

Call: 
hhh4(stsObj = noroBE, control = ctrl3)

Coefficients:
                        Estimate   Std. Error
ar.1.chwi               -2.984424   1.350606 
ar.1.frkr               -1.546018   0.255272 
ar.1.lich               -1.481704   0.269704 
ar.1.mahe               -1.042180   0.165513 
ar.1.mitt               -1.684145   0.325195 
ar.1.neuk               -1.178880   0.203516 
ar.1.pank               -0.950771   0.162474 
ar.1.rein               -0.739190   0.113666 
ar.1.span               -1.030189   0.159685 
ar.1.zehl               -0.700978   0.109133 
ar.1.scho               -1.140107   0.188365 
ar.1.trko               -0.954548   0.156077 
ne.1.chwi               -1.556838   0.229854 
ne.1.frkr               -2.105432   0.303360 
ne.1.lich               -1.333358   0.275089 
ne.1.mahe               -2.082596   1.001100 
ne.1.mitt               -1.382118   0.285452 
ne.1.neuk               -1.005697   0.308230 
ne.1.pank               -0.594043   0.265078 
ne.1.rein               -1.531222   0.365439 
ne.1.span               -1.496264   0.237766 
ne.1.zehl               -1.197674   0.519991 
ne.1.scho               -1.174415   0.268474 
ne.1.trko               -2.805666   1.088384 
end.sin(2 * pi * t/52)   0.013954   0.037300 
end.cos(2 * pi * t/52)   0.918633   0.033880 
end.1.chwi               0.817175   0.143907 
end.1.frkr               0.142450   0.200990 
end.1.lich               0.636253   0.176280 
end.1.mahe               0.715465   0.135111 
end.1.mitt               0.541823   0.187192 
end.1.neuk               0.444922   0.175794 
end.1.pank               0.867238   0.188664 
end.1.rein               0.349285   0.222273 
end.1.span               0.143326   0.183118 
end.1.zehl               1.068714   0.140279 
end.1.scho               0.730291   0.182337 
end.1.trko               0.866186   0.143240 
overdisp                 0.182920   0.009464 

Log-likelihood:   -8596.56 
AIC:              17271.12 
BIC:              17513.37 

Number of units:        12 
Number of time points:  307 
AIC(fit3)
[1] 17271.12

You can explore the importance of the neighbourhood component by re-plotting the model fits.

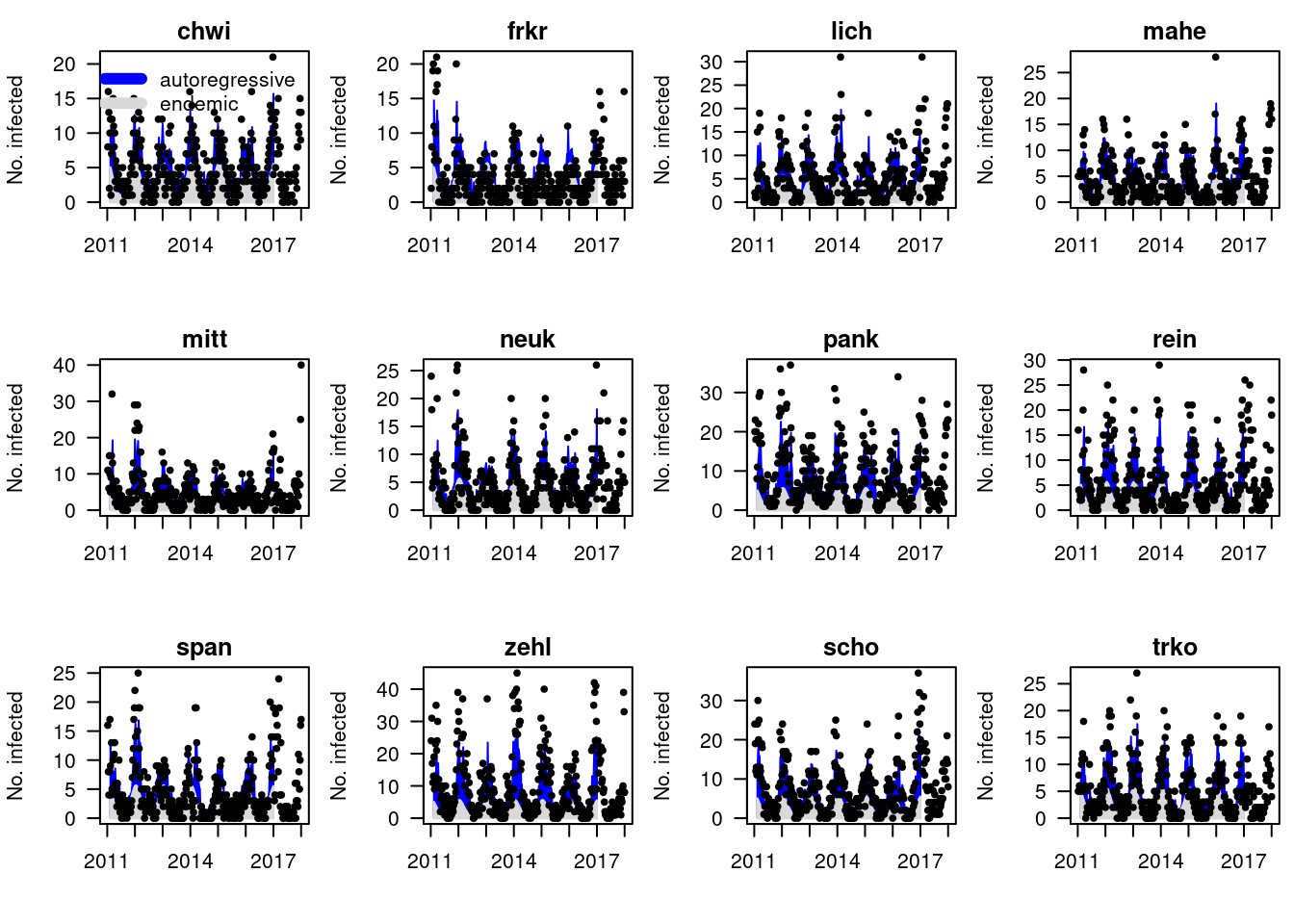
Solution 
plot(fit3, unit = 1:12)
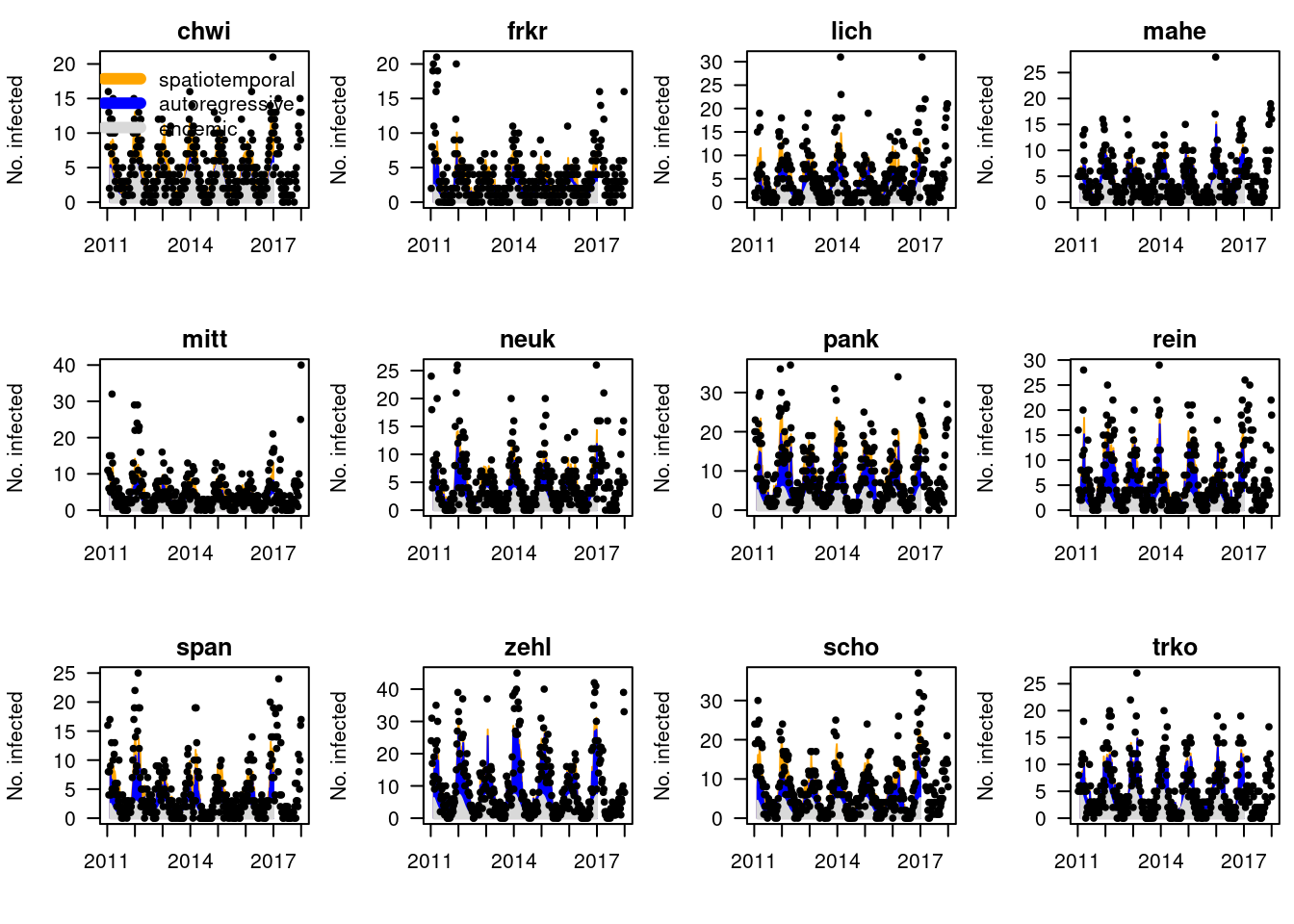Plotting the model fits, we see that for certain districts the neighbourhood component is very important (chwi), for others negligible (trko). This may be due to poor identifiability (often the autoregressive terms from the same and other districts are strongly correlated).

Step 4: Using a power law for spatial dependence.

The above formulation requires a lot of parameters as the autoregressions on the same and other regions are handled separately. Moreover, it only takes into account direct neighbours. A more parsimonious model also allowing for dependencies between indirect neighbours is a power-law formulation, where we set \[\begin{align} \mu_{it} & = \nu_{it} + \lambda_i Y_{i, t - 1} + \phi_i \sum_{j = 1}^K w_{ji} Y_{j, t - 1} \end{align}\] with weights \(w_{ji}\) defined as follows.

  • if normalize == FALSE: \[ w_{ji} = (o_{ji} + 1)^{-\rho} \].
  • if normalize == TRUE: \[ w_{ji} = \frac{(o_{ji} + 1)^{-\rho}}{\sum_{i = 1}^K (o_{jk} + 1)^{-\rho}}$ \] Here, \(o_{ji}\) is the path distance between districts \(j\) and \(i\), i.e., the entries of noroBE@neihbourhood.
Click for an intuitive visual sketch of this model

Returning to our simple illustration with three districts, this step adds some additional connections between indirect neighbours (districts 1 and 3). They are shown in light grey as by construction of the model they are weaker than those between neighbouring districts.

Try to add a power law with normalization to the model (see ?W_powerlaw).

Some hints
  • If you want to fit the model as described above, your control list should no longer contain an ar element.
  • The maxlagargument does not play much of a role in this toy examples, you can e.g., set it to 5.
Solution 
##################################################################
# Model 4

# For the next model version we will formally include the autoregressive into
# the neighbourhood component
# (i.e. do no longer treat autoregression on the same district separately). 
# This can be done as follows.
# First we need to adapt the neighbourhood matrix, shifting by one
noroBE_power <- noroBE
noroBE_power@neighbourhood <- noroBE@neighbourhood + 1

# new control argument:
ctrl4 <- list(end = list(f = addSeason2formula(~0 + fe(1, unitSpecific = TRUE),
                                               S = 1)),
              # note: line ar = ... is removed
              ne = list(f = ~0 + fe(1, unitSpecific = TRUE),
                        weights = W_powerlaw(maxlag=5, normalize = TRUE,
                                             log = TRUE)), # this is new
              family = "NegBin1",
              subset = subset_fit)
# normalize = TRUE normalizes weights by the number of neighbours of the
# exporting district
# log = TRUE means optimization will be done on a  log scale, ensuring 
# positivity of the decay parameter (which is desirable)
fit4 <- hhh4(noroBE_power, ctrl4)
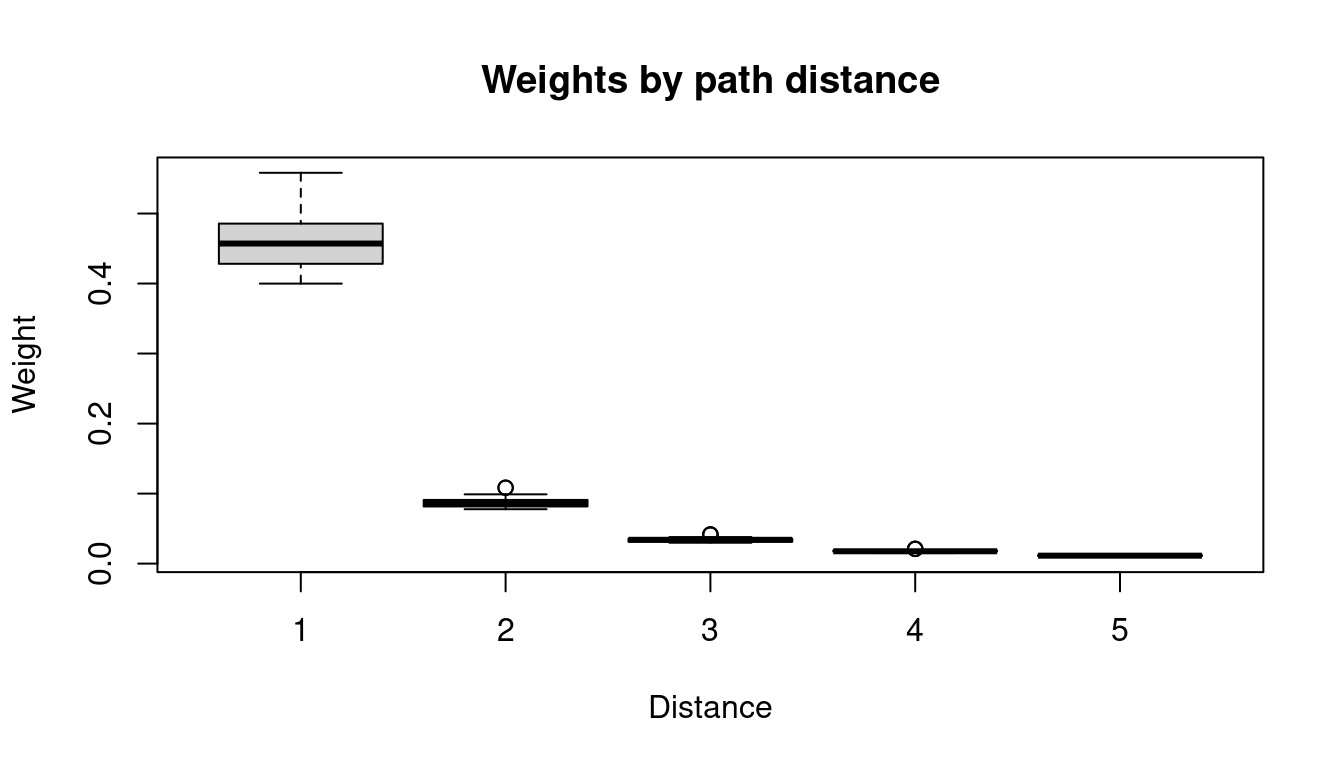
AIC(fit4)
[1] 17233.06
## This yields a quite drastic improvement in AIC.

We can visualize the weights \(w_{ji}\) as a function of the path dependence \(o_{ji}\) (see ?plot.hhh4).

Solution 
# visualize the nighbourhood weights:
plot(fit4, type = "neweights", main = "Weights by path distance")

Step 5: Adding seasonality to the epidemic component.

Including seasonality in the ar and ne components when both are present can lead to identifiability issues. In the more parsimonious model where only the ne component is present, however, including seasonal terms here can considerably improve the model fit. Extend the previous model to include seasonal terms (with S = 1) in the necomponent.

Solution 
##################################################################
# Model 5:
ctrl5 <- list(end = list(f = addSeason2formula(~0 + fe(1, unitSpecific = TRUE),
                                               S = 1)),
              # now adding seasonality to the ne component:
              ne = list(f =  addSeason2formula(~0 + fe(1, unitSpecific = TRUE),
                                               S = 1),
                        weights = W_powerlaw(maxlag=5, normalize = TRUE,
                                             log=TRUE)), # this is new
              family = "NegBin1",
              subset = subset_fit)
fit5 <- hhh4(noroBE_power, ctrl5)
AIC(fit5)
[1] 17205.41

Bonus steps

If you have made it until here before the session is over – congratulations! Below you will find some additional ideas to keep you busy. They do not have a specific ordering and you can try them out independently of each other.

Bonus: Adding higher-order lags.

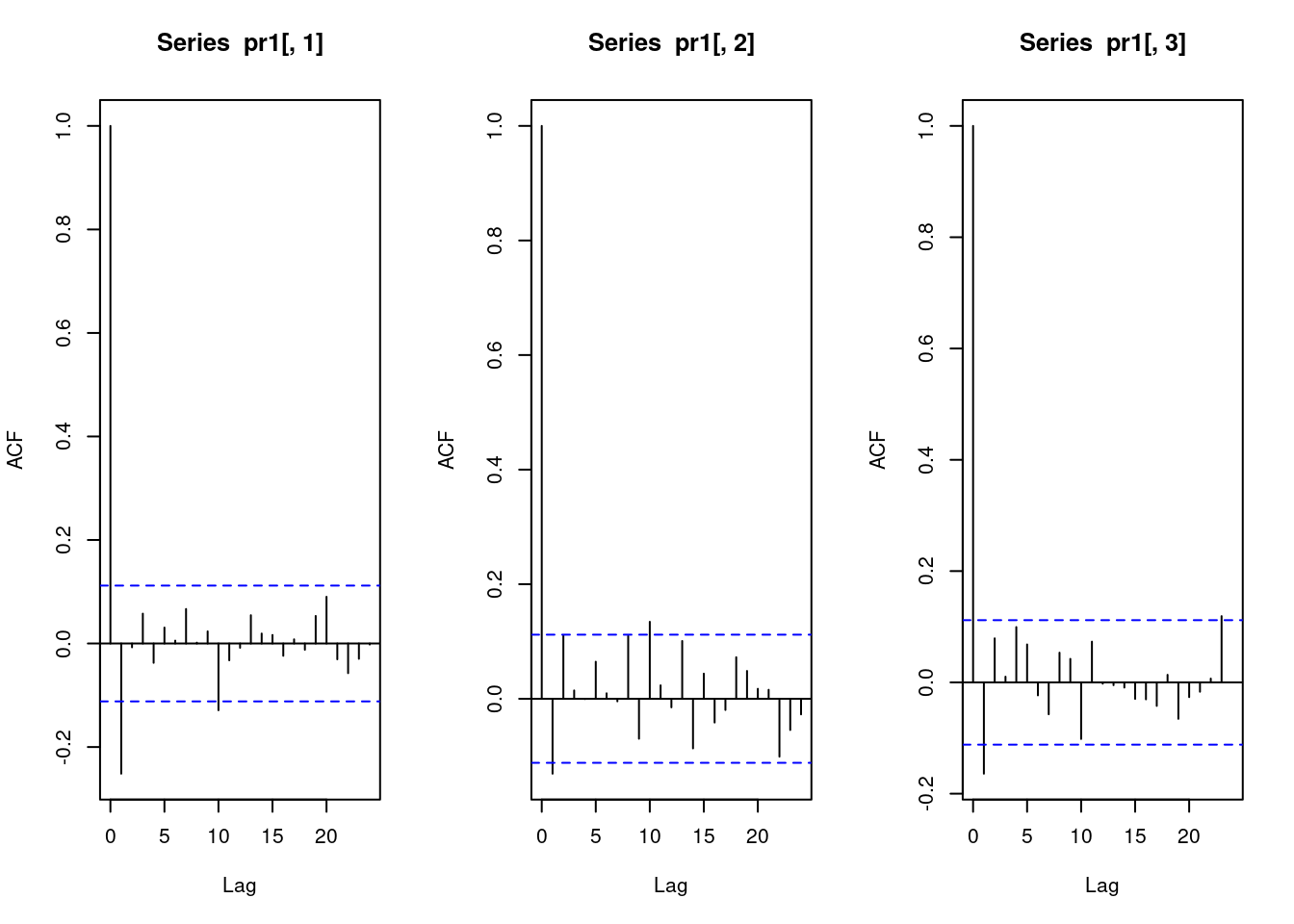
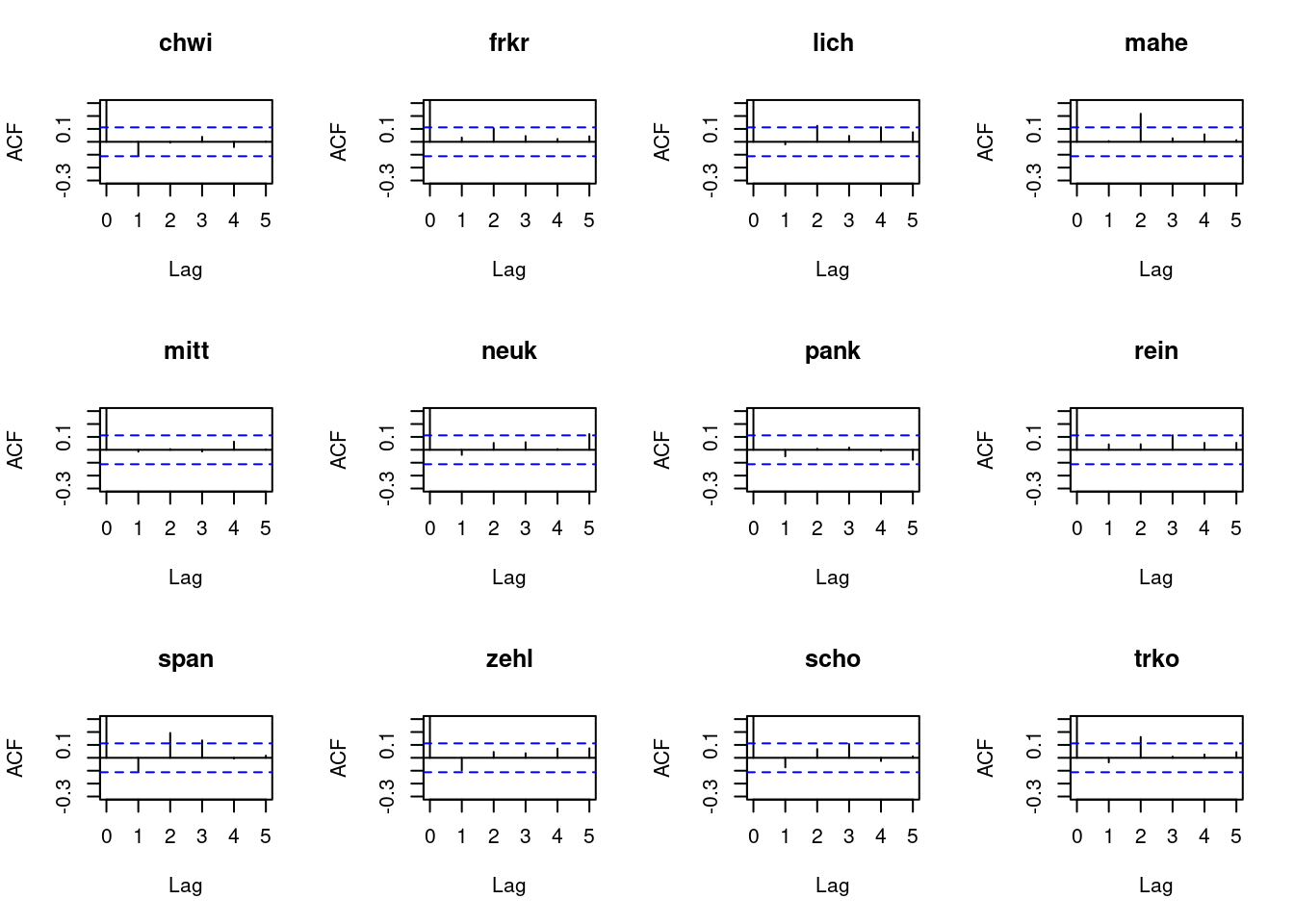
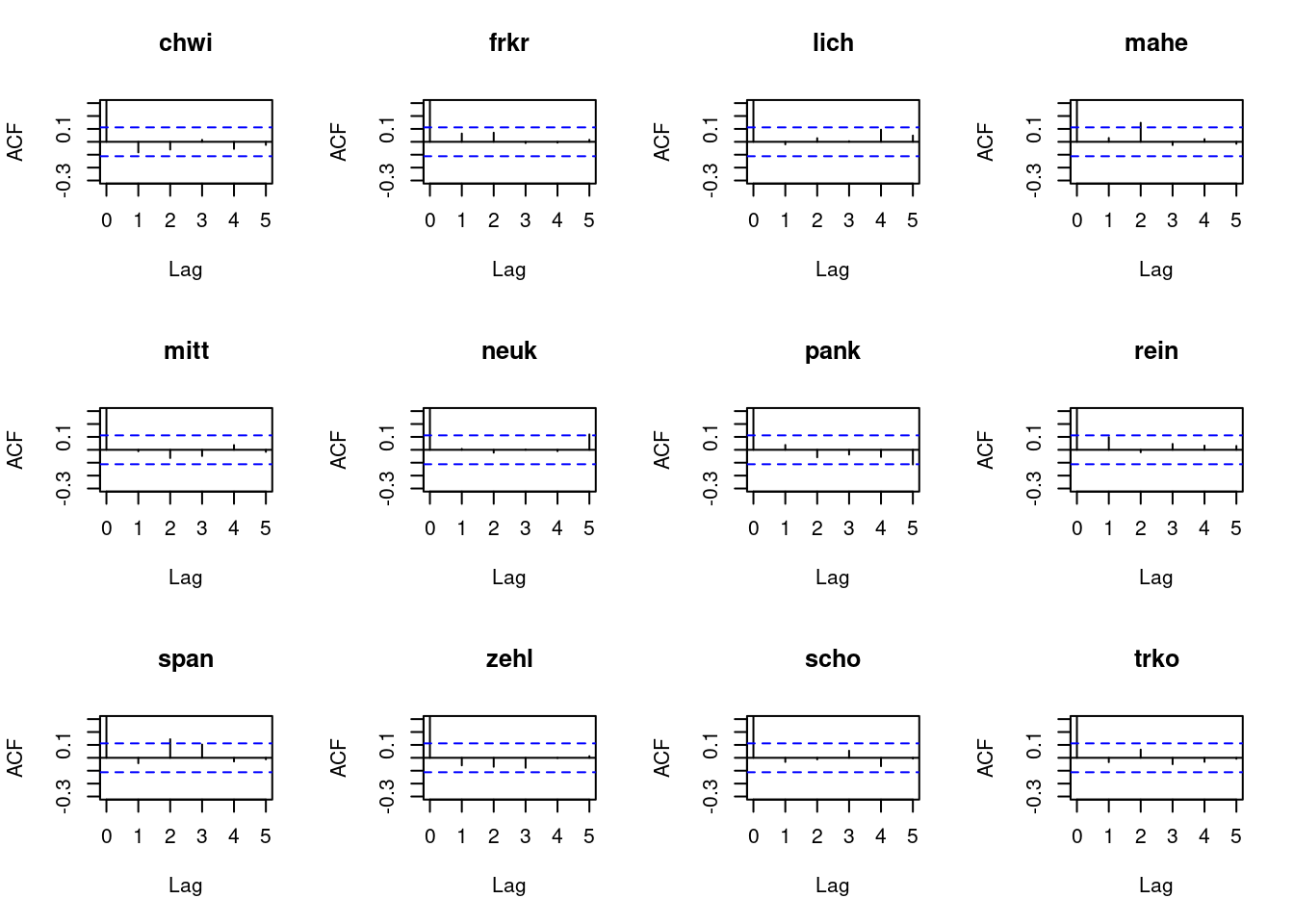
Let us re-consider the autocorrelation of the Pearson residuals. You will see that for several regions there are pronounced residual autocorrelations at lags 2 or 3, indicating that there is additional information to be exploited.

Solution 
# compute Pearson residuals:
pr5 <- pearson_residuals(fit4)
par(mfrow = c(3, 4))
for(unit in colnames(pr5)){
  acf(pr5[, unit], lag.max = 5, ylim = c(-0.3, 0.3), main = unit)
}

To remedy this, higher-order lags can be included in the model. This functionality is implemented in the hhh4addon package. For technical reasons this package is not on CRAN, but you can install it from GitHub.

## to install hhh4addon:
# install.packages("remotes")
# remotes::install_github("jbracher/hhh4addon", build_vignettes = TRUE)

library(hhh4addon)
Registered S3 methods overwritten by 'hhh4addon':
  method                from        
  confint.oneStepAhead  surveillance
  plot.oneStepAhead     surveillance
  quantile.oneStepAhead surveillance
This is a development version of hhh4addon. It modifies and extends functionalities of surveillance:hhh4.

Attache Paket: 'hhh4addon'
Das folgende Objekt ist maskiert 'package:surveillance':

    decompose.hhh4

The model then becomes

\[ \mu_{it} = \nu_{it} + \lambda_i Y_{i, t - 1} + \phi_i \sum_{j = 1}^K \sum_{d = 1}^D u_d w_{ji} Y_{j, t - 1}. \]

Lag weights are (usually) governed by a single parameter, which is fed into a function returning the weights. The package contains the several parsimonious parameterizations (?profile_par_lag), e.g.,:

  • geometric: \(\tilde{u}_d = \alpha(1 - \alpha)^{d - 1}\)
  • Poisson: \(\tilde{u}_d = \alpha^{d - 1}\exp(-\alpha)/(d - 1)!\)

The lag weights are standardized so they sum up to one, setting \(u_d = \tilde{u}_d / \sum_{i = 1}^D \tilde{u}_{i}\). In mechanistic interpretation, they correspond to the generation time / serial interval distribution.

Click for an intuitive visual sketch of this model

Returning a last time to our toy illustration of three districts, this step adds a whole lot of (typically weak) connections between non-neighbouring time points.

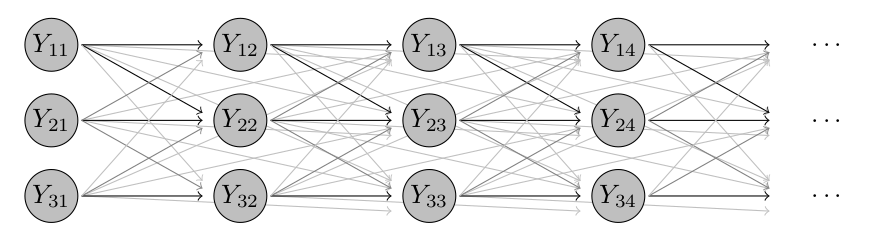
Try to fit a model with geometric lag weights (the default) using the function profile_par_lag. Then re-check the Pearson residuals.

Why does this function have such a strange name? Orininally there was afunction hhh4lag which allowed for lag weights specified by the user and typically based on literature estimates of the generation time distribution. Functionality to estimate the a weighting parameter \(\alpha\) was only added later and is based on a profile likelihood approach. As this parameter is called par_lag in the implementation, the function running profile likelihood inference is called profile_par_lag.
Solution 
##################################################################
# Model 7
ctrl7 <- list(end = list(f = addSeason2formula(~0 + fe(1, unitSpecific = TRUE),
                                               S = 1)),
              # note: line ar = ... is removed
              ne = list(f = addSeason2formula(~0 + fe(1, unitSpecific = TRUE),
                                              S = 1),
                        weights = W_powerlaw(maxlag=5, normalize = TRUE,
                                             log=TRUE)), # this is new
              family = "NegBin1",
              subset = subset_fit,
              # (no specification of par_lag in the control)
              funct_lag = geometric_lag)
# now use profile_par_lag (applies a profile likelihood procedure to estimate
# the lag decay parameter)
fit7 <- profile_par_lag(noroBE_power, ctrl7)
AIC(fit7)
[1] 17138.12

We can plot the weights as estimated from the data:

# plot the weights assigned to the different lags:
par(mfrow = 1:2)
plot(fit7$distr_lag, type = "h", xlab  = "lag",
     ylab = "weight", ylim = 0:1)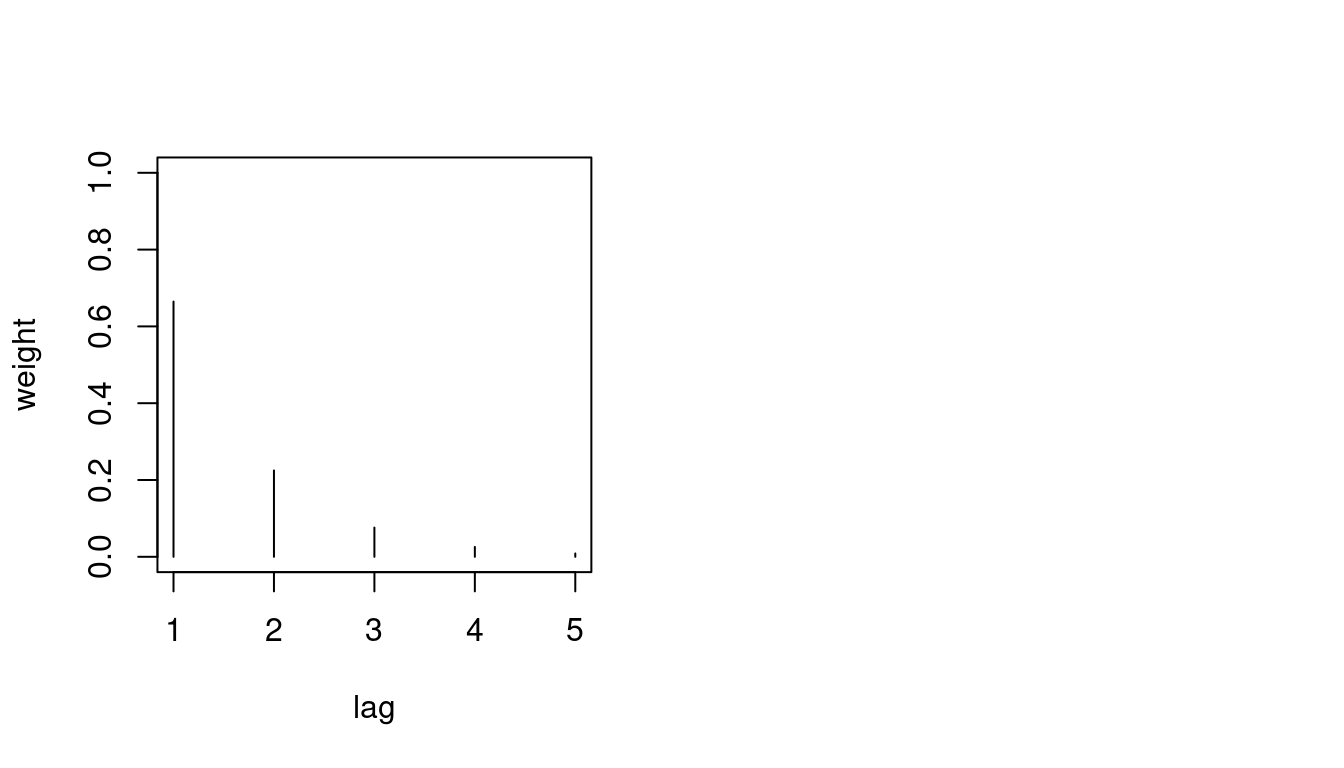

And consider the Pearson residuals, which look less problematic than before.

# check Pearson residuals
pr7 <- pearson_residuals(fit7)
par(mfrow = c(3, 4))
for(unit in colnames(pr7)){
  acf(pr7[, unit], lag.max = 5, ylim = c(-0.3, 0.3), main = unit)
}

Bonus: One-step-ahead forecasting.

The packages contain functionality to imitate one-step-ahead (out-of-sample) forecasts retrospectively. To this end, the model is sequentially re-fitted, always including all data up to a given week. Then a one-week-ahead plug-in prediciton is obtained for the next week. We apply this to obtain predictions for weeks 313 through 364 which we had excluded from model fitting so far. Subsequently, you can use scores to evaluate the one-step-ahead predictions using several different scoring rules. We compute the following:

  • the logarithmic score, also called negative predictive log-likelihood (informal explanation: this reflects how likely the observed outcomes were under your predictions)
  • the CRPS (informal explanation: this describes “how far” the observations were from the predictions you issued)

For both lower values are better.

As this may be a bit tedious to piece together I am providing the analysis for fit2 and fit4 and you can explore things based on this skeleton.

Find the code here 
##################################################################
# one-step-ahead forecasting: generate forecasts sequentially
# compare models 2, 4 and 7
log2 <- capture.output(owa2 <- oneStepAhead(fit2, tp = c(312, 363)))
log4 <- capture.output(owa4 <- oneStepAhead(fit4, tp = c(312, 363)))
rm(log2, log4)
# the weird capture.output fourmulation is needed to suppress 
# numerous cat() messages.
# you could also just use
# owa2 <- oneStepAhead(fit2, tp = c(312, 363))
owa7 <- oneStepAhead_hhh4lag(fit7, tp = c(312, 363))
Lag weights are not re-estimated for the one-step-ahead forecasts (set refit_par_lag = TRUE to re-fit them).
# the return objects contain predictions, observations and a few other things:
head(owa7$pred)
         chwi     frkr      lich     mahe      mitt      neuk     pank     rein      span     zehl
313 10.143891 5.997015  8.315079 7.550797 12.276675  9.072281 18.06990 12.35556 13.161304 20.62583
314 10.052363 6.133326  9.568715 7.025105 12.332588 11.455435 20.52966 10.66938 10.103430 23.18901
315 10.837812 6.638302 10.085745 8.250180 10.817444 10.246092 22.11388 17.05596  8.692397 24.61323
316  9.737658 6.614878 16.126879 8.251785  8.842089  8.346344 24.43109 14.89341  7.391036 19.24499
317  8.017484 5.761749 10.387913 6.531485  6.529512  7.030808 20.62327 11.56332 10.879236 19.91117
318  9.328702 7.435577 13.008535 6.949797  8.054874  9.280143 20.39342 11.20380 11.205468 19.68513
        scho     trko
313 19.19221 7.951694
314 18.21469 8.461257
315 21.20857 8.030405
316 17.81345 7.817094
317 14.02415 6.814946
318 16.13912 8.639782
head(owa7$observed)
    chwi frkr lich mahe mitt neuk pank rein span zehl scho trko
313   10    4   10    5   17   16   23    5    7   24   17    5
314   12    8    9   10    6    8   23   26    3   24   28    3
315   11    7   31    7    3    5   28   14    4   14   18    2
316    5    8    6    5    0    5   22    8   18   20   12    4
317   13   16   20    6    7   11   20    8   14   17   18    6
318    7    8    7    5    3   16    9   20   12   22   31   11
# plot one-step-ahead point forecasts:
plot(noroBE@observed[313:364, 1], pch = 20, xlab = "week", ylab = "value")
lines(owa2$pred[, 1], type = "l", col = 2)
lines(owa4$pred[, 1], type = "l", col = 4)
lines(owa7$pred[, 1], type = "l", col = 6)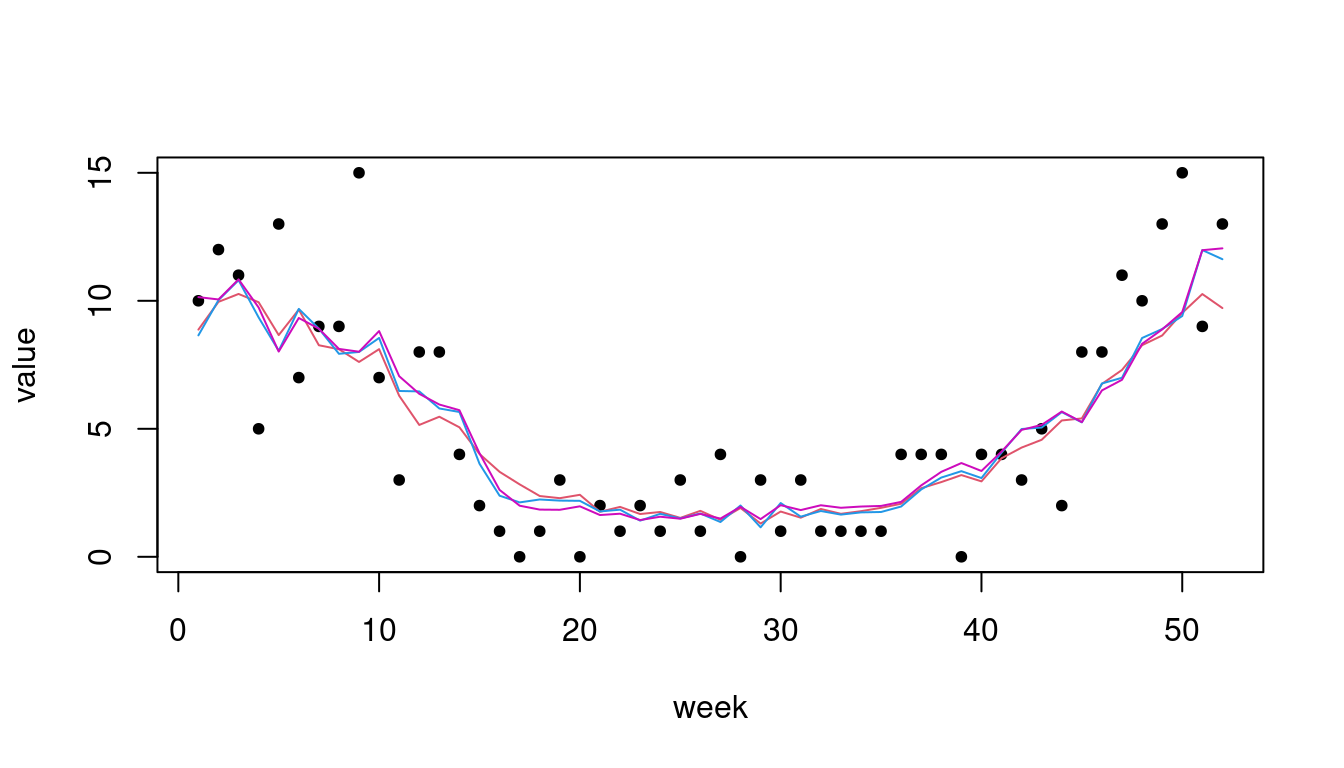

# compute and summarize scores:
colMeans(scores(owa2, which = c("logs", "rps")))
    logs      rps 
2.506608 2.091024 
colMeans(scores(owa4, which = c("logs", "rps")))
    logs      rps 
2.492431 2.066390 
colMeans(scores(owa7, which = c("logs", "rps")))
    logs      rps 
2.475311 2.042008

We can see that the more complex model formulations also translate to improved predictive performance (all scores being negatively oriented; see ?scores).

Bonus: Including a covariate.

Norovirus transmission has been argued to depend on meteorological variables including temperature. We therefore uploaded a time series of weekly mean temperature values in Berlin (average of daily temperatures at 2pm, lagged by one week) in the data bundle for the workshop. These (or a transformation) can be used a a covariate.

data_temperature <- read.csv("data/temperature_berlin.csv")
temperature <- data_temperature$temperature7d

Try to include these in the model in a way you think might be helpful.

Find my minimal attempt here

I would assume temperature to modify the transmissibility of the virus, so I included the covariate into the ar component of a simple model.

# your formula could look as follows:
ctrl_temp <- list(end = list(f = addSeason2formula(~0 + fe(1, unitSpecific = TRUE),
                                              S = 1)),
             ar = list(f = ~ 0 + temperature + fe(1, unitSpecific = TRUE)),
             family = "NegBin1",
             subset = 6:312)


fit_temp <- hhh4(noroBE, ctrl_temp)
AIC(fit_temp)
[1] 17318.05
# for comparison:
AIC(fit2)
[1] 17364.92
This indeed leads to an improvement in AIC over fit2, which is the same model just without the covariate. Up to you to check this in more complex models.

Please keep in mind that this is a toy example to allow you to explore the hhh4 framework, not a serious analysis of norovirus epidemiology.