Data

We use data from routine surveillance in Germany carried out by Robert Koch Institute. We have already prepared these as "sts" (surveillance time series) data, which you can directly load from the provided RData file.

library("surveillance")
Lade nötiges Paket: sp
Lade nötiges Paket: xtable
This is surveillance 1.23.1; see 'package?surveillance' or
https://surveillance.R-Forge.R-project.org/ for an overview.
load("data/data_BE.RData", verbose = TRUE)
Loading objects:
  noroBE
  rotaBE

We focus on noroBE, which contains weekly counts of confirmed cases of norovirus gastroenteritis in Berlin, 2011–2017, stratified by district. These data have already been used as an example in at least two publications on hhh4 extensions (for serial interval distributions and social contact data, respectively).

The rotaBE dataset contains the same for rotavirus gastroenteritis, which you can explore if you want to play around a bit more.

In this tutorial, we only look at the overall time series aggregated over all districts:

noro <- aggregate(noroBE, by = "unit")
noro
-- An object of class sts -- 
freq:        52 
start:       2011 1 
dim(observed):   364 1 

Head of observed:
     overall
[1,]     157
Task

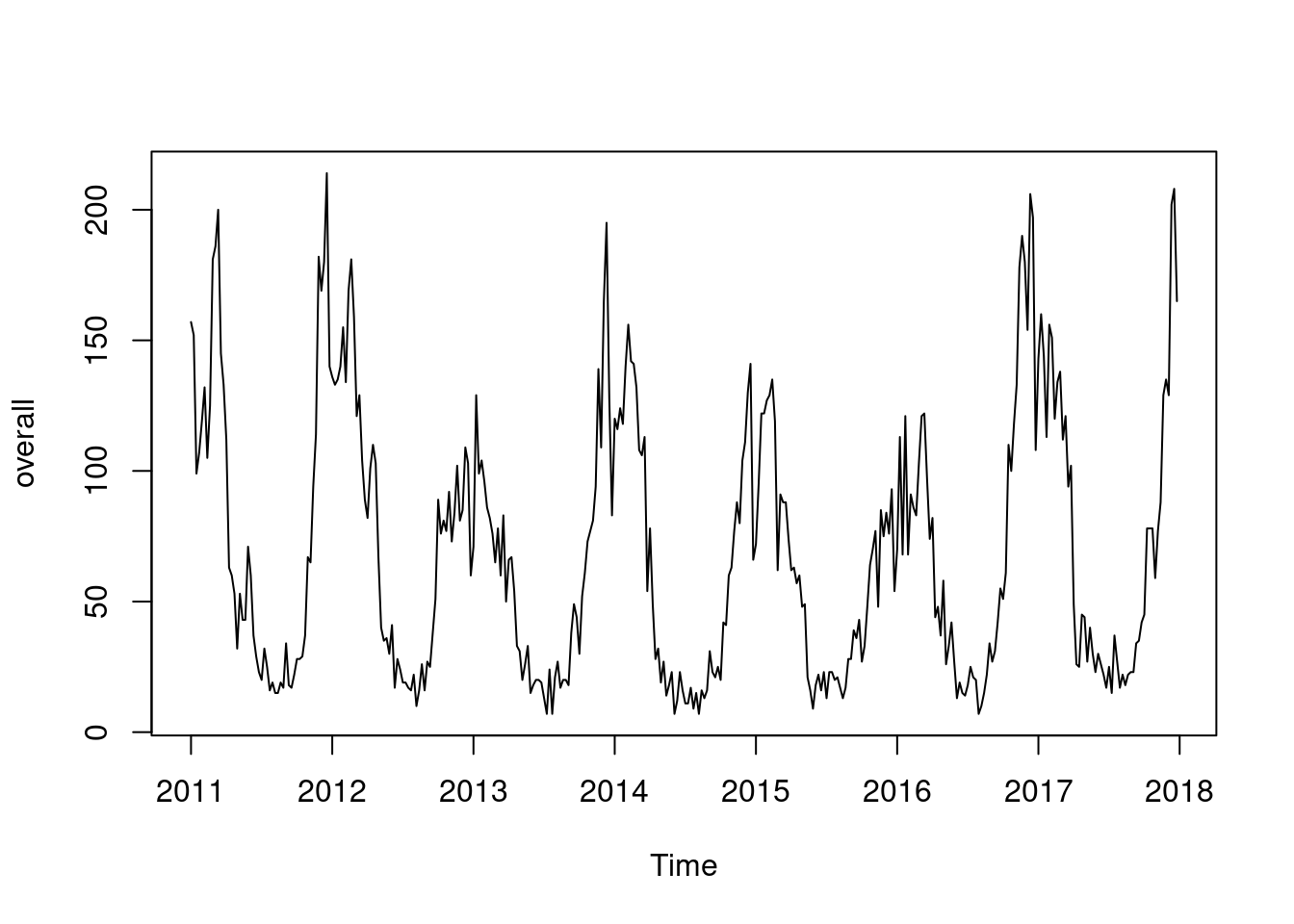
Look at a plot() of the data. You can also try a ggplot2 version via ggplot2::autoplot(), or plot an as.ts() or xts::as.xts() (if you have that) version of the data.

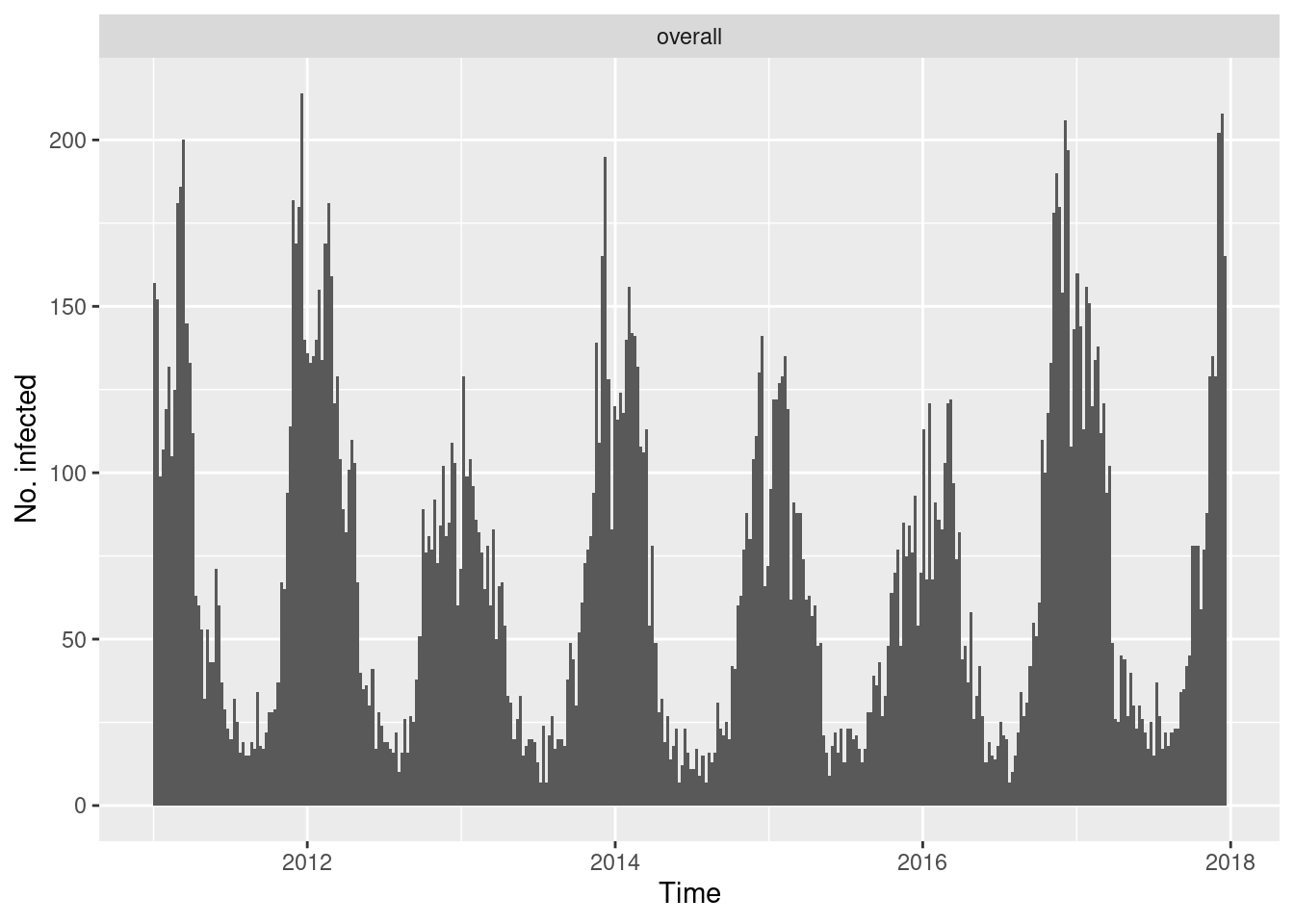
Alternatively, convert the "sts" object to a “tidy” data frame via tidy.sts() and use your favourite plotting tool.

Solution 
plot(noro)

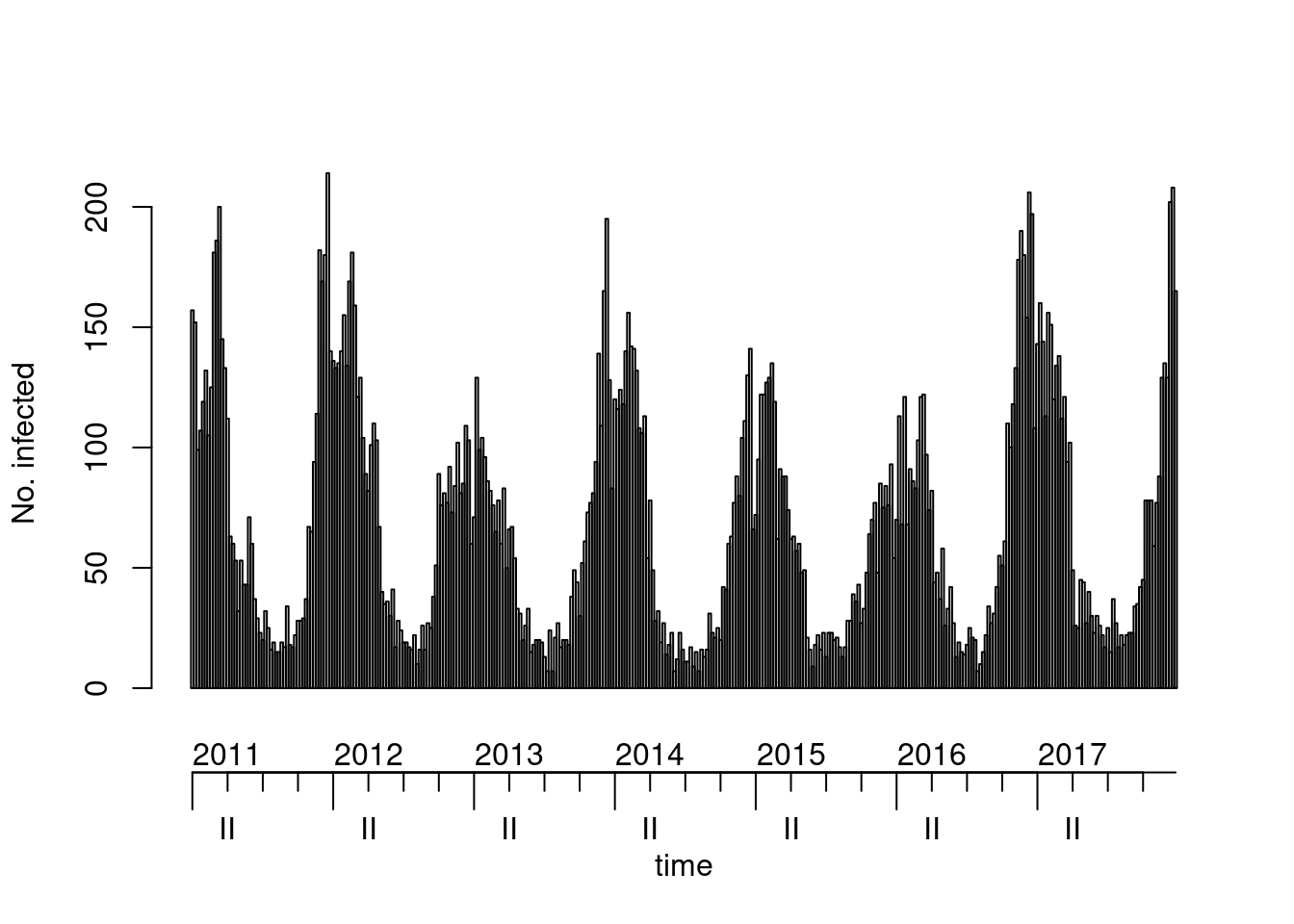
## alternative visualizations (and there are probably more)
plot(noro, col = 8, epochsAsDate = TRUE)  # alternative colour & time axis setup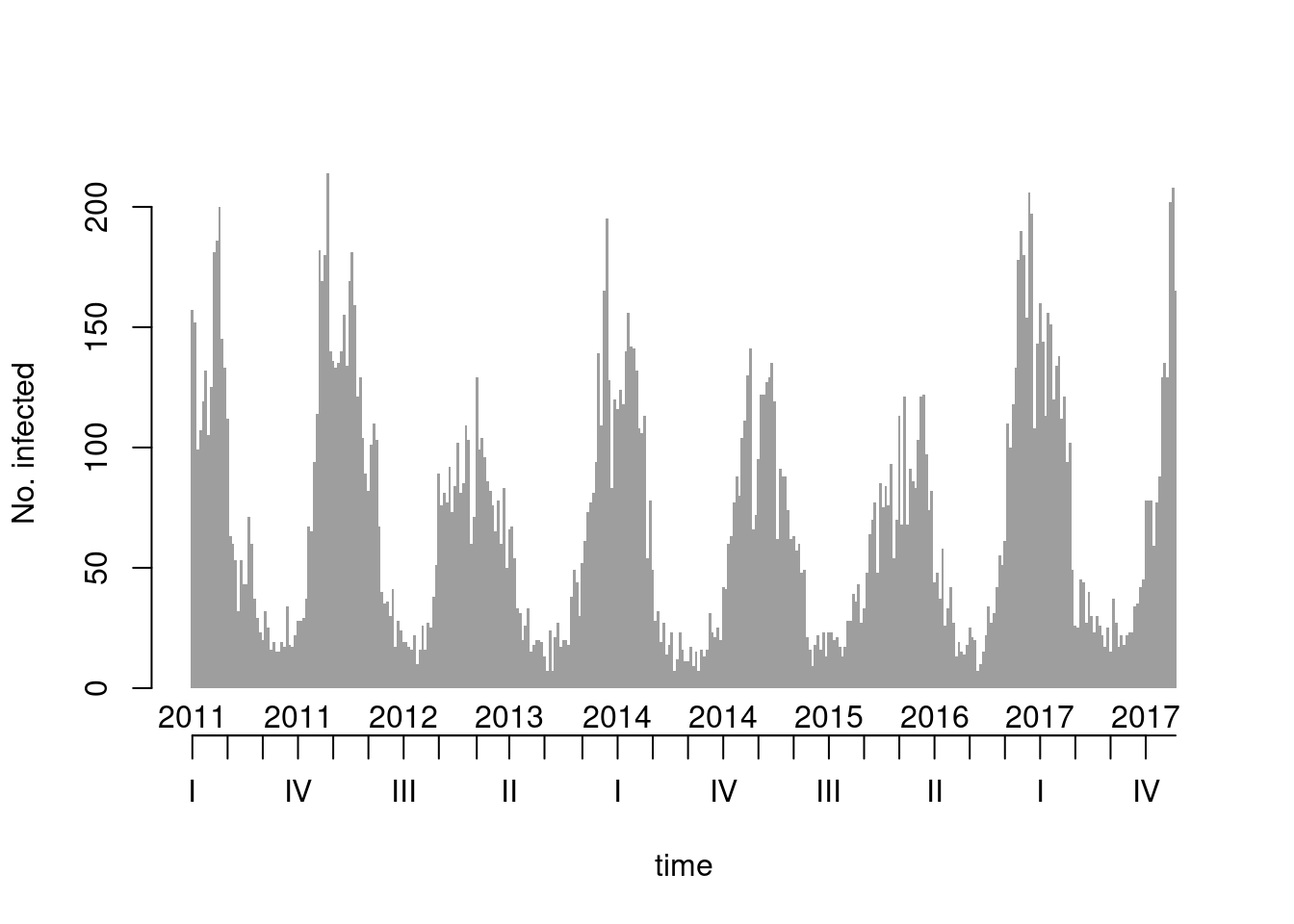

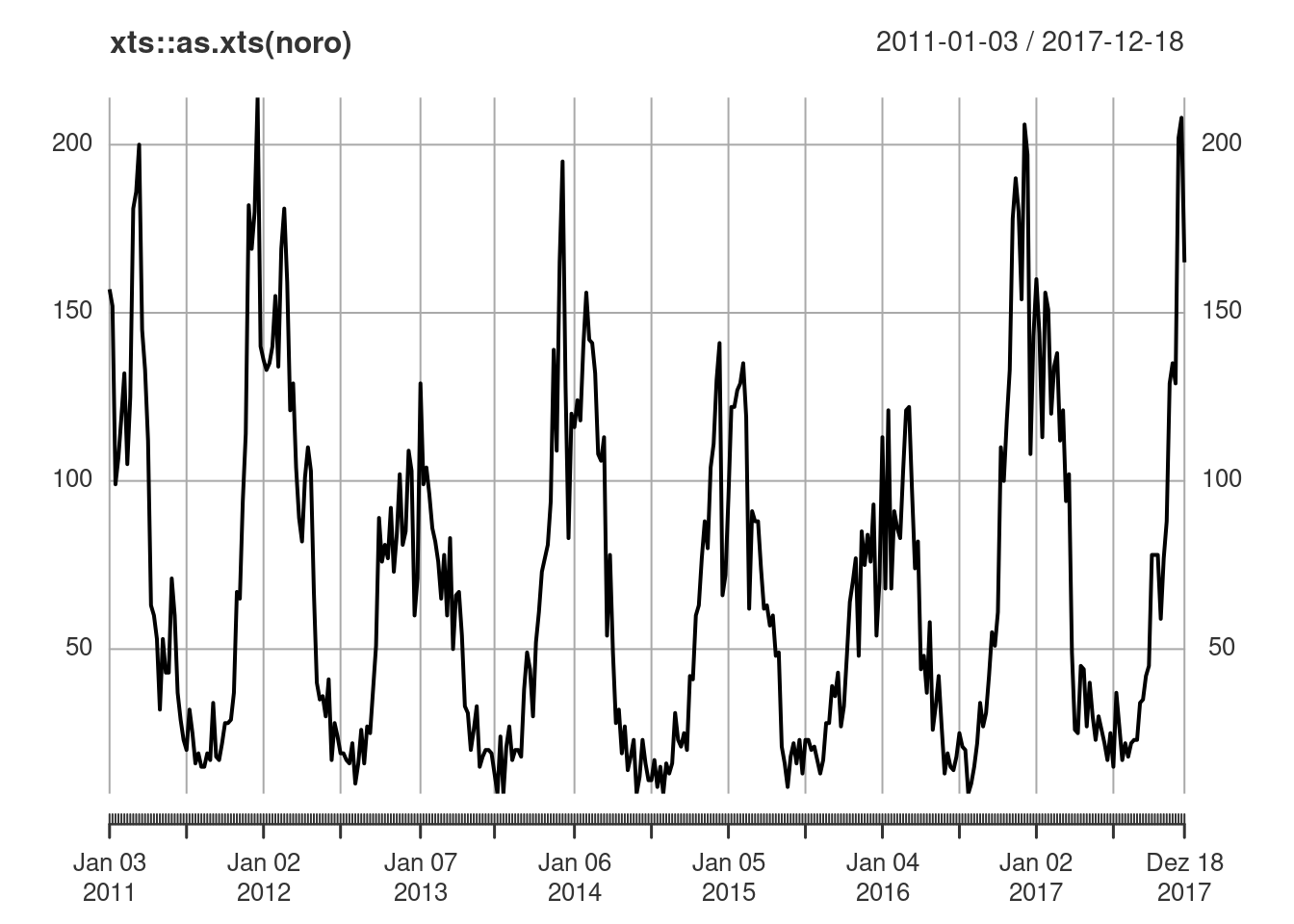
plot(as.ts(noro))

ggplot2::autoplot(noro)

plot(xts::as.xts(noro))

## there is a clear yearly seasonality, see also
## the basic "ts" monthplot()
as.ts(noro) |> monthplot(lwd.base = 3)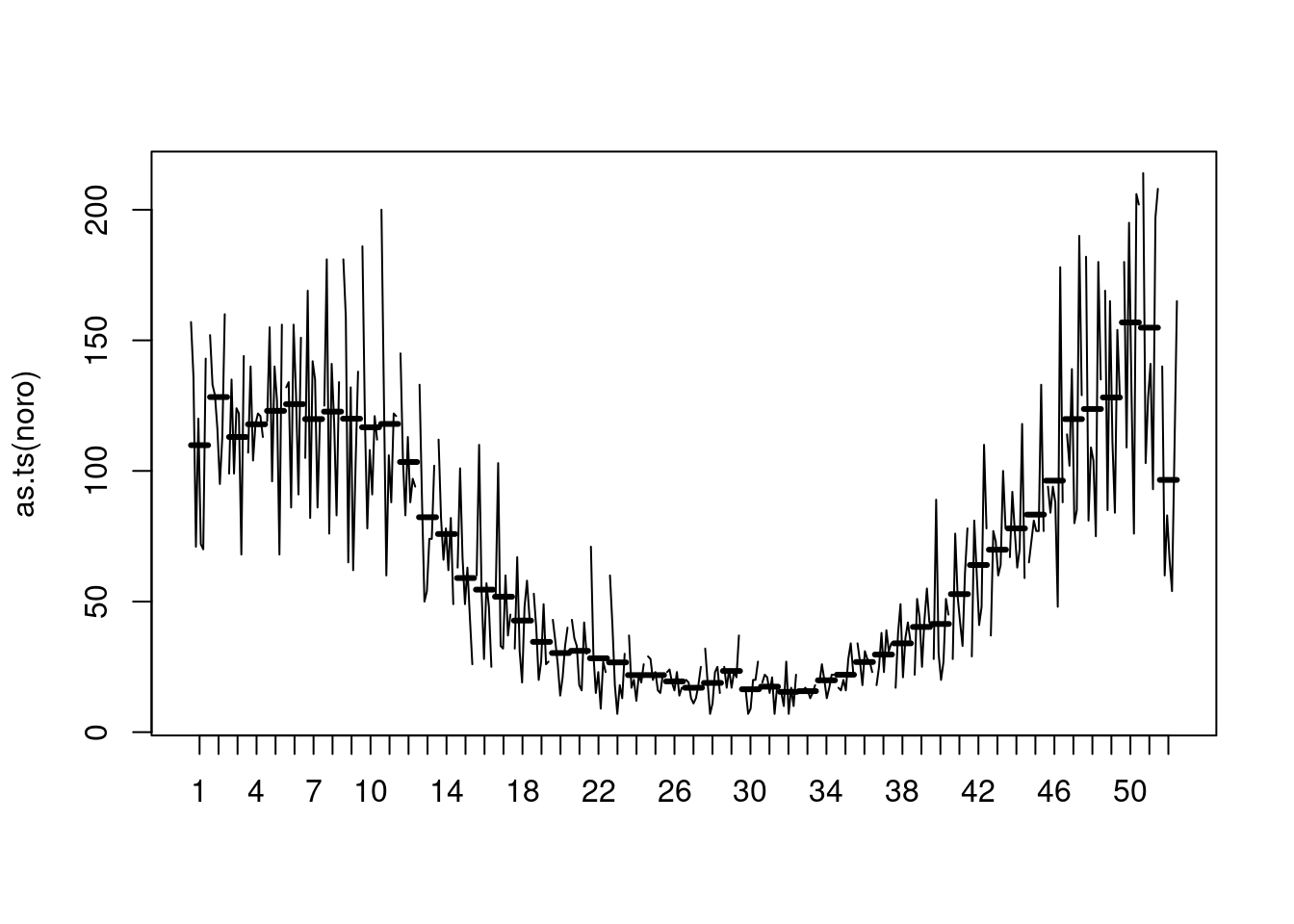

## => (unfortunate) peak around Christmas, minimum around calendar week 32

## or use, e.g., lattice::xyplot() with the "tidy" dataset
lattice::xyplot(observed ~ epochInYear, data = tidy.sts(noro),
                groups = year, type = "l", xlab = "calendar week")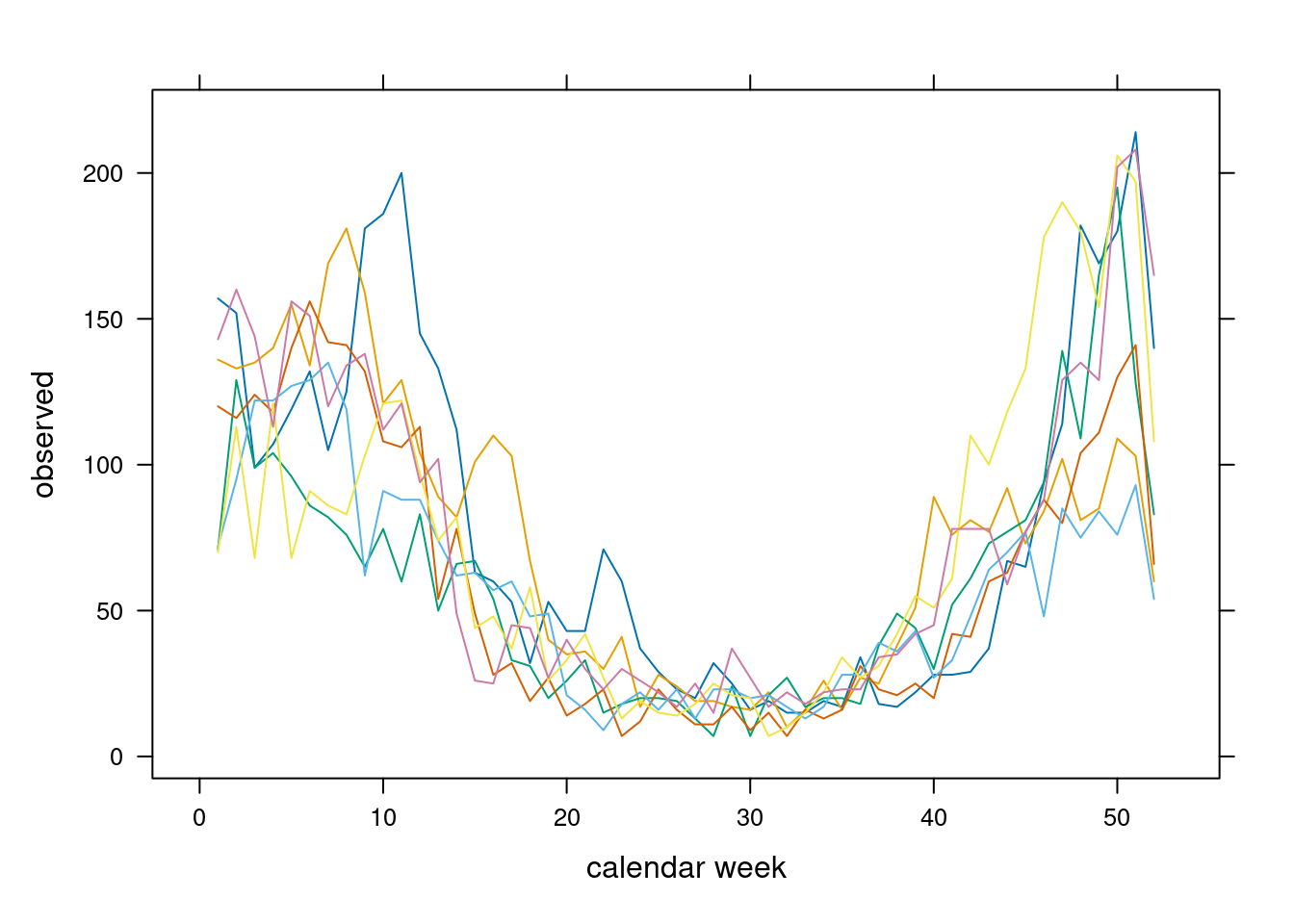

Fitting hhh4() models

We don’t have any exogenous covariates in this example, but we can at least capture seasonality by including transformations of time (pairs of sine-cosine terms) as covariates in the model.

In statistical terms, we will fit simple models of the form

\[ Y_t | Y_{t-1} \sim \operatorname{NegBin}(\nu_t + \lambda_t y_{t-1}, \phi) \]

where the log-linear predictors \(\nu_t\) (endemic component) and \(\lambda_t\) (ar component) could use regression formulae of the form

\[ \alpha + \sum_{s=1}^S \left\{ \gamma_s \sin(s \omega t) + \delta_s \cos(s \omega t) \right\} \]

with S harmonics of “fundamental frequency” \(\omega=2\pi/52\).

Such a formula for use in hhh4() model components can be created very easily, here adding just one harmonic to an intercept-only formula:

f1 <- addSeason2formula(~ 1, S = 1, period = 52)
f1
~1 + sin(2 * pi * t/52) + cos(2 * pi * t/52)

The basic syntax for fitting an endemic-epidemic time-series model is

fit <- hhh4(stsObj, control)

where the first argument gives the data as an "sts" object (here: noro) and the second argument specifies the model in the form of a list. For example, the rudimentary intercept-only model NegBin\((\nu + \lambda y_{t-1}, \phi)\) could be specified using the following control list:

control = list(
    ar  = list(f = ~ 1),
    end = list(f = ~ 1),
    family = "NegBin1"
)
Task

Estimate a few different hhh4() models with seasonality (e.g., using f = f1 from above) and compare them using AIC(fit1, fit2, ....) (Akaike Information Criterion, smaller is better).

Note that you can update() a previously fitted model and only specify what you would like to change. For example, if fit was the intercept-only model from above, you could estimate a new model where the autoregressive component uses the f1 formula as follows:

fit2 <- update(fit, ar = list(f = f1))
Solution 
## try an endemic-only model with one harmonic
fit_endemic <- hhh4(noro, list(end = list(f = f1), family = "NegBin1"))

## try the intercept-only endemic-epidemic model
fit00 <- hhh4(noro, list(ar = list(f = ~1), end = list(f = ~1), family = "NegBin1"))

## try various options with seasonality
fit01 <- update(fit00, S = list(ar = 0, end = 1))  # constant lambda
fit10 <- update(fit00, S = list(ar = 1, end = 0))  # constant nu
fit11 <- update(fit00, S = list(ar = 1, end = 1))  # both seasonal

AIC(fit_endemic, fit00, fit01, fit10, fit11)
            df      AIC
fit_endemic  4 3151.523
fit00        3 3057.533
fit01        5 2969.641
fit10        5 2991.624
fit11        7 2966.411
## 'fit11' wins, but the more parsimonious 'fit01' is pretty close

Inspecting the fit

The list of methods(class = "hhh4") is quite long. Some useful ones for inspecting model fits are summary(), plot() (see ?plot.hhh4), pit(), and residuals().

Task

Inspect some of the fitted models.

Solution 
## show the coefficients with standard errors:
summary(fit01)

Call: 
hhh4(stsObj = object$stsObj, control = control)

Coefficients:
                        Estimate   Std. Error
ar.1                    -0.481167   0.065909 
end.1                    3.010150   0.102923 
end.sin(2 * pi * t/52)   0.032159   0.058467 
end.cos(2 * pi * t/52)   1.010425   0.049928 
overdisp                 0.051619   0.005481 

Log-likelihood:   -1479.82 
AIC:              2969.64 
BIC:              2989.11 

Number of units:        1 
Number of time points:  363 
## transform sine-cosine coefficients to amplitude-shift parameters,
## exp-transform the intercepts to get to the response scale,
## and show the dominant eigenvalue ("=" epidemic proportion)
summary(fit01, amplitudeShift = TRUE, idx2Exp = TRUE, maxEV = TRUE)

Call: 
hhh4(stsObj = object$stsObj, control = control)

Coefficients:
                      Estimate   Std. Error
exp(ar.1)              0.618062   0.040736 
exp(end.1)            20.290441   2.088360 
end.A(2 * pi * t/52)   1.010937   0.051310 
end.s(2 * pi * t/52)   1.538980   0.031096 
overdisp               0.051619   0.005481 

Epidemic dominant eigenvalue:  0.62 

Log-likelihood:   -1479.82 
AIC:              2969.64 
BIC:              2989.11 

Number of units:        1 
Number of time points:  363 
## epidemic proportion of disease incidence is estimated to be 62%
## the rest isn't necessarily non-epidemic, but imported/unexplained

## show the fitted model components
plot(fit01) -> .components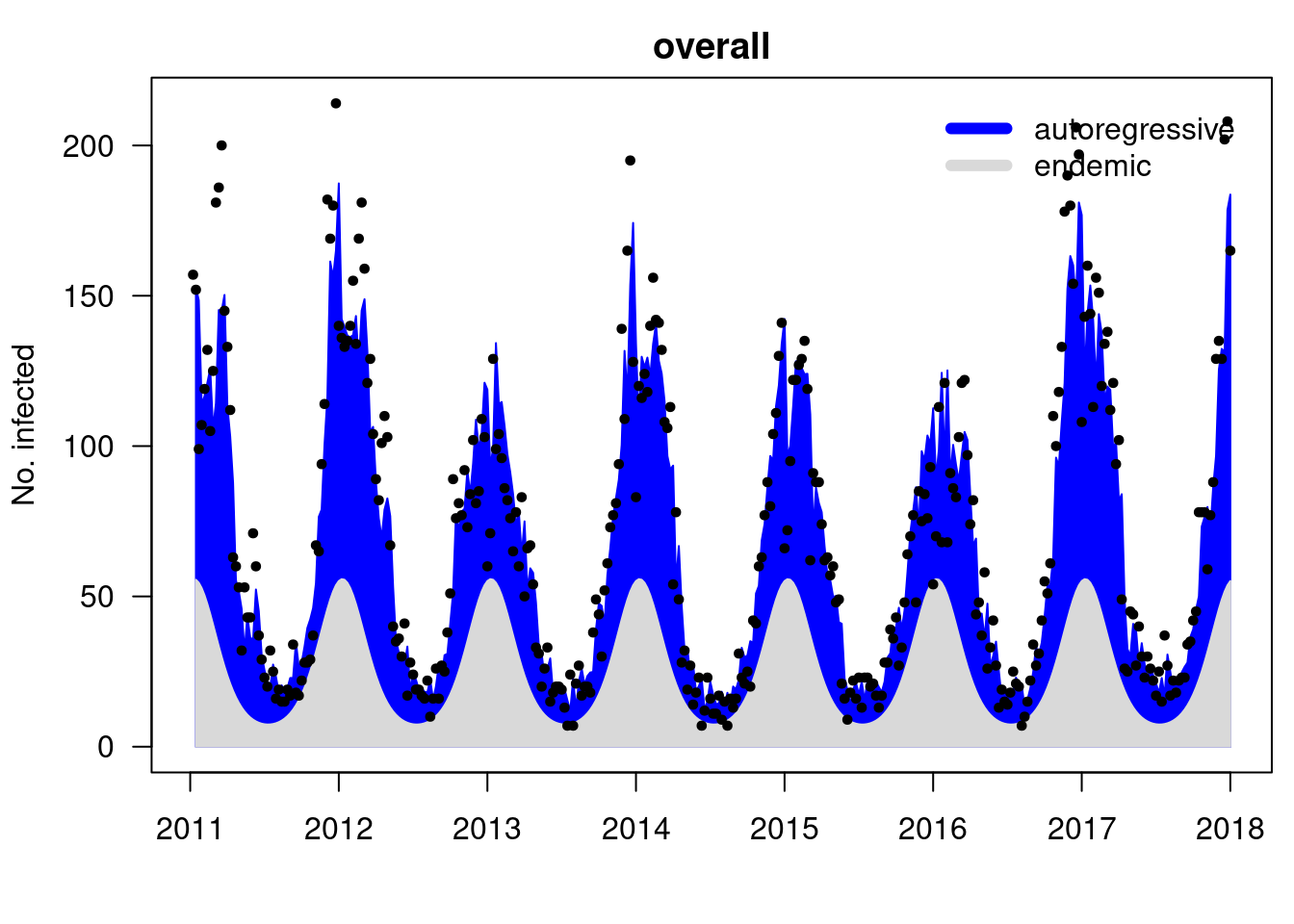

## calculate the "empirical" epidemic proportion
str(.components)
List of 1
 $ overall: num [1:363, 1:8] 153 148 114 117 121 ...
  ..- attr(*, "dimnames")=List of 2
  .. ..$ : NULL
  .. ..$ : chr [1:8] "mean" "epidemic" "endemic" "epi.own" ...
sum(.components$overall[,"epidemic"]) / sum(.components$overall[,"mean"])
[1] 0.6210123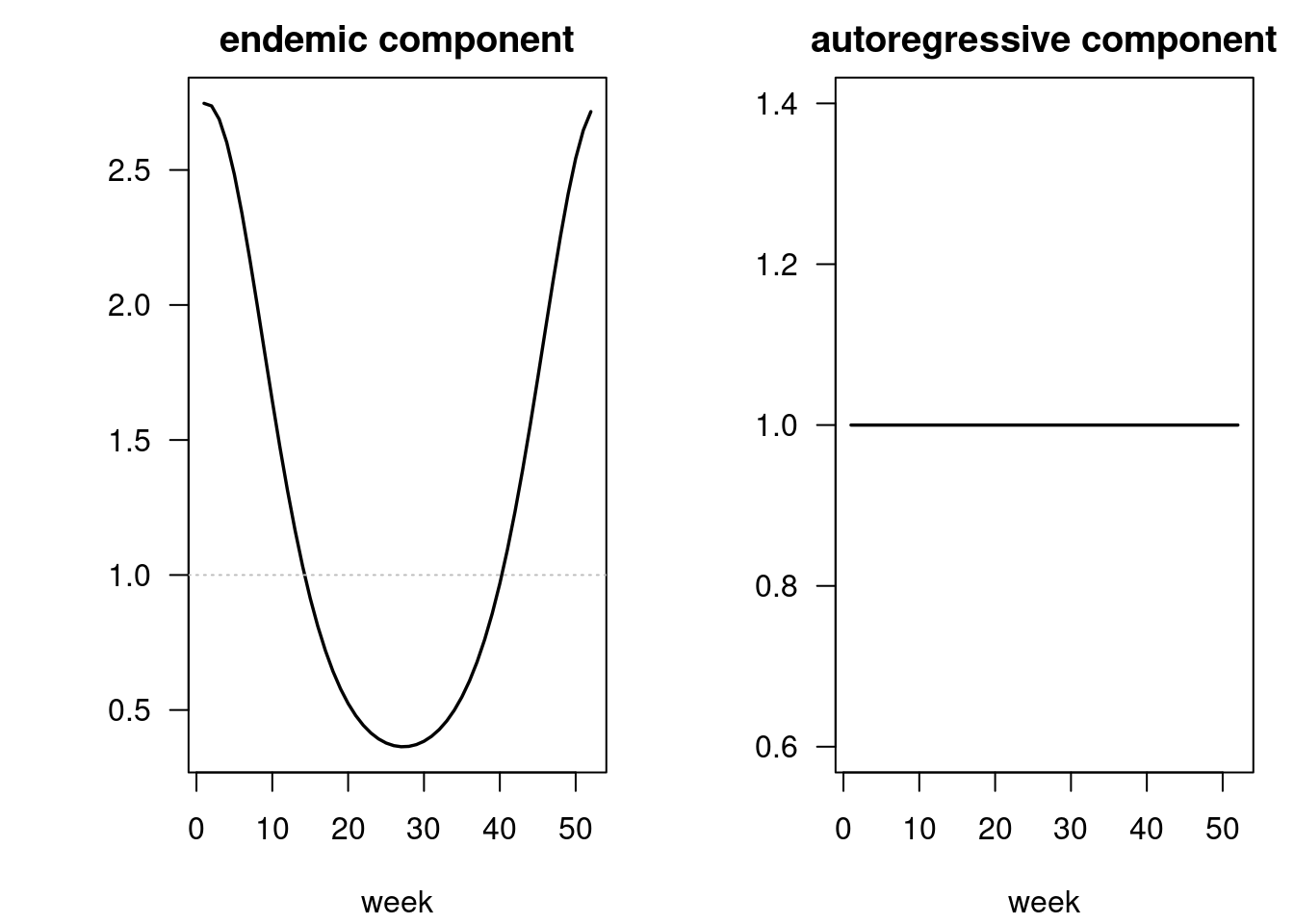
## show the estimated seasonal (multiplicative) effect
plot(fit01, type = "season")

## PIT plot to check model calibration
opar <- par(mfrow = c(1,2))
pit(fit01); title(main = "constant lambda")
pit(fit11); title(main = "seasonal lambda")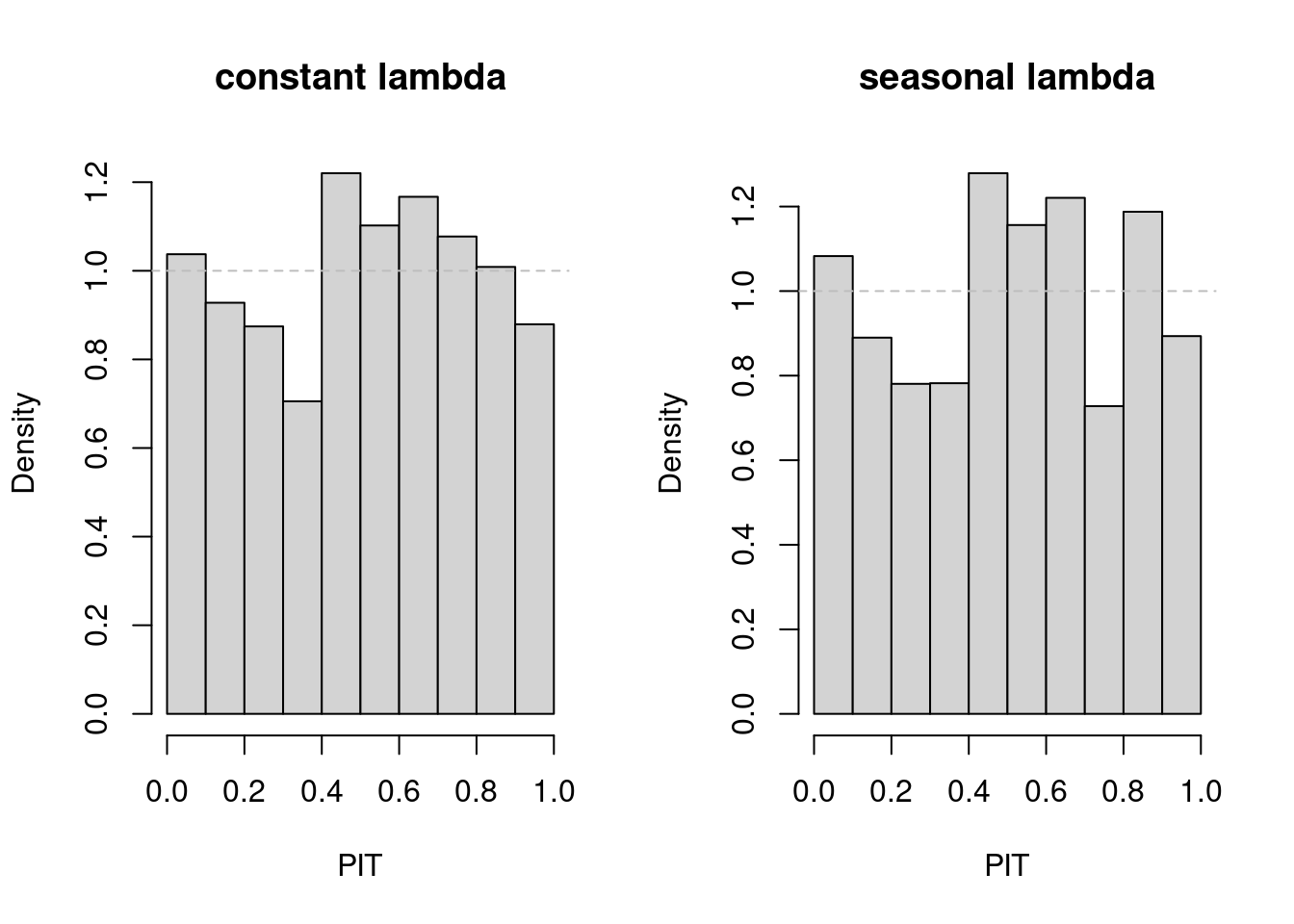

par(opar)
## no clear preference

## check residual correlation
opar <- par(mfrow = c(1,3))
acf(residuals(fit_endemic), main = "endemic-only") # strong residual correlation
acf(residuals(fit01), main = "constant lambda")
acf(residuals(fit11), main = "seasonal lambda")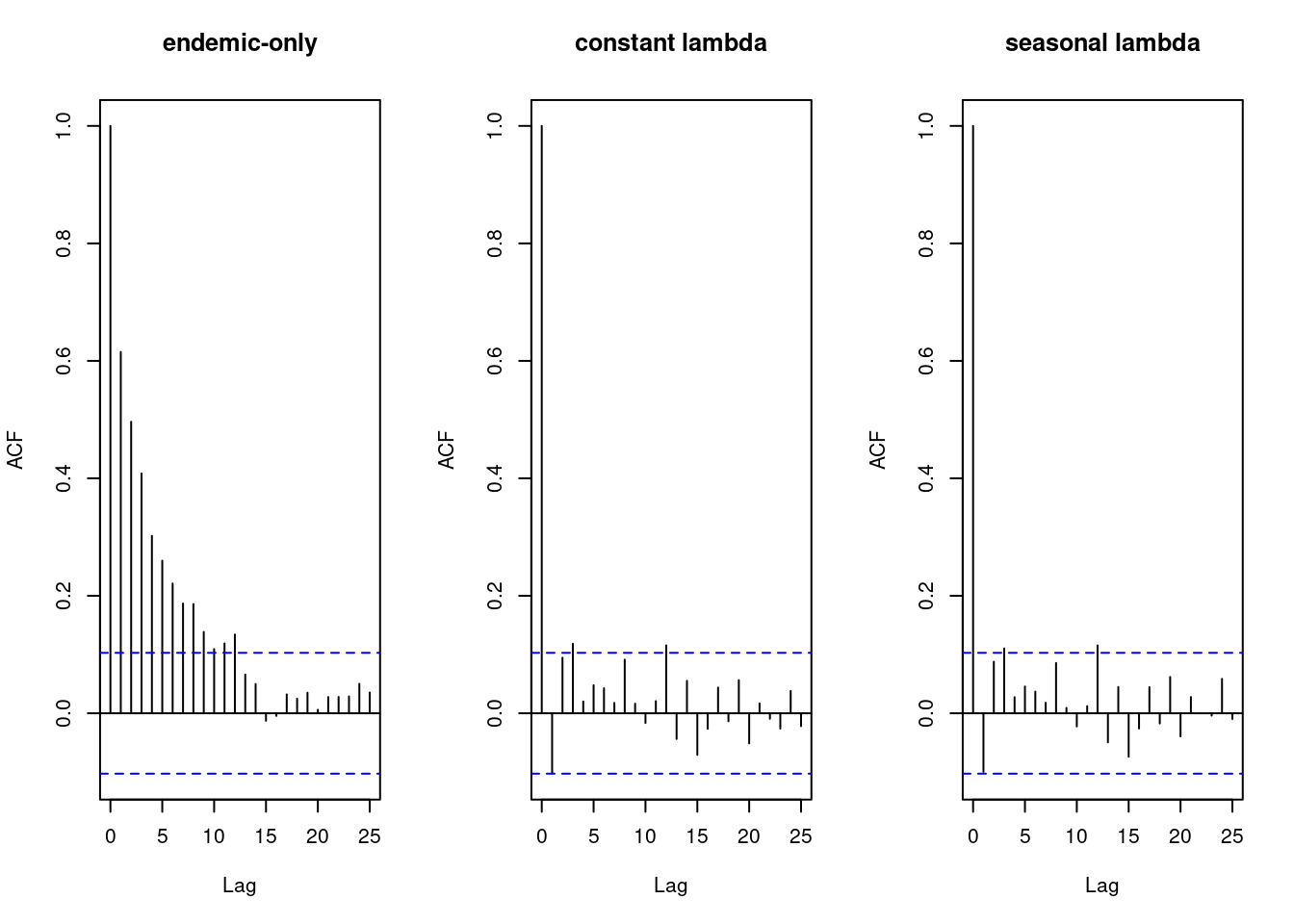

par(opar)
## no clear preference either

Forecasting

Task

Use oneStepAhead() to produce “rolling” weekly forecasts, e.g., over the last two years, and plot() the result. You should also look at a pit() histogram of these probabilistic forecasts.

Solution 
## compute "rolling" weekly forecasts starting from 2016
startidx <- match(2016, year(noro))
osa01 <- oneStepAhead(fit01, startidx, verbose = FALSE)
plot(osa01)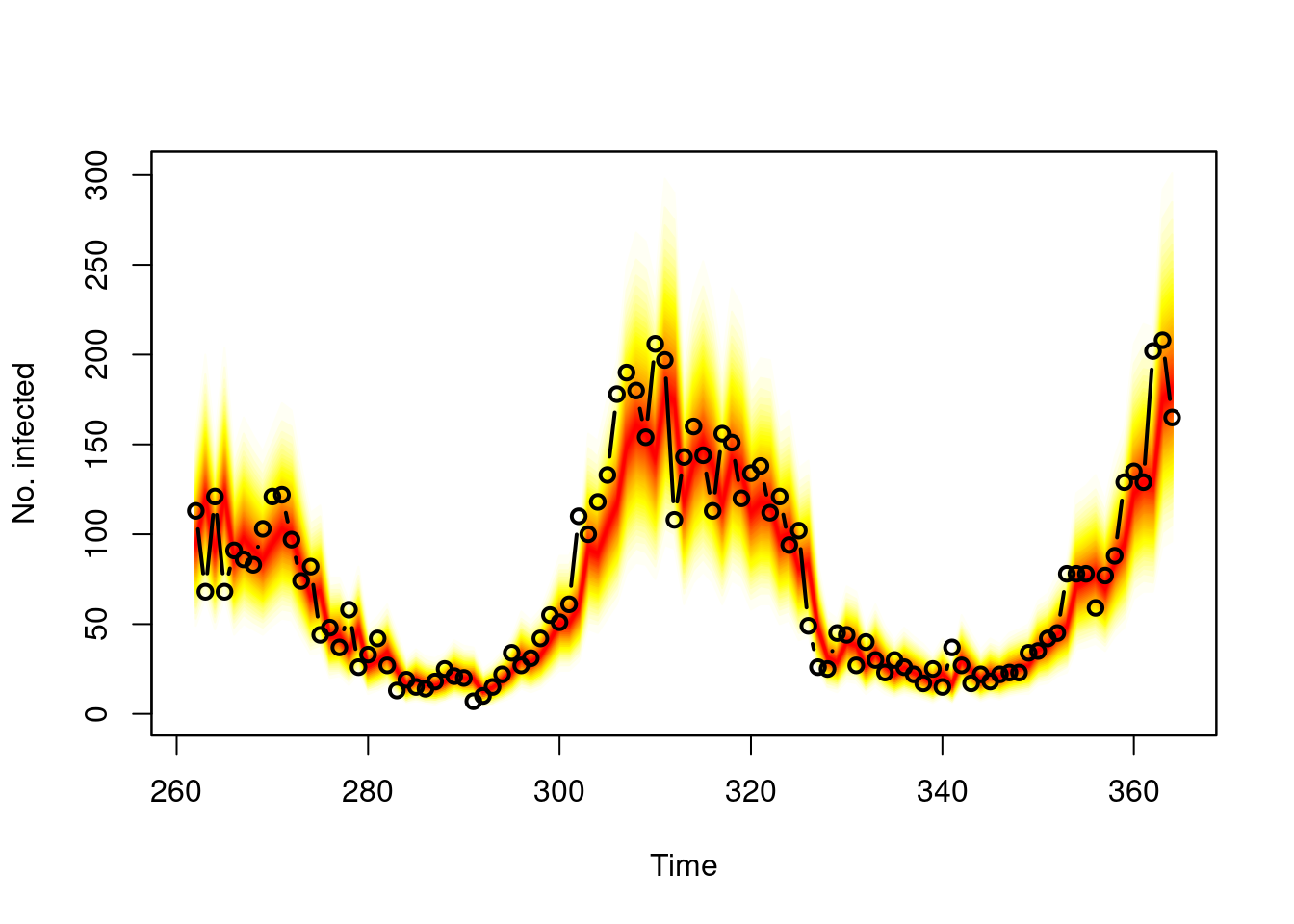

head(quantile(osa01)) # median and prediction intervals
    2.5 % 10.0 % 50.0 % 90.0 % 97.5 %
262    55     67     94    127    147
263    71     86    120    161    186
264    53     64     91    123    142
265    71     87    122    164    189
266    50     61     87    118    137
267    56     69     98    132    153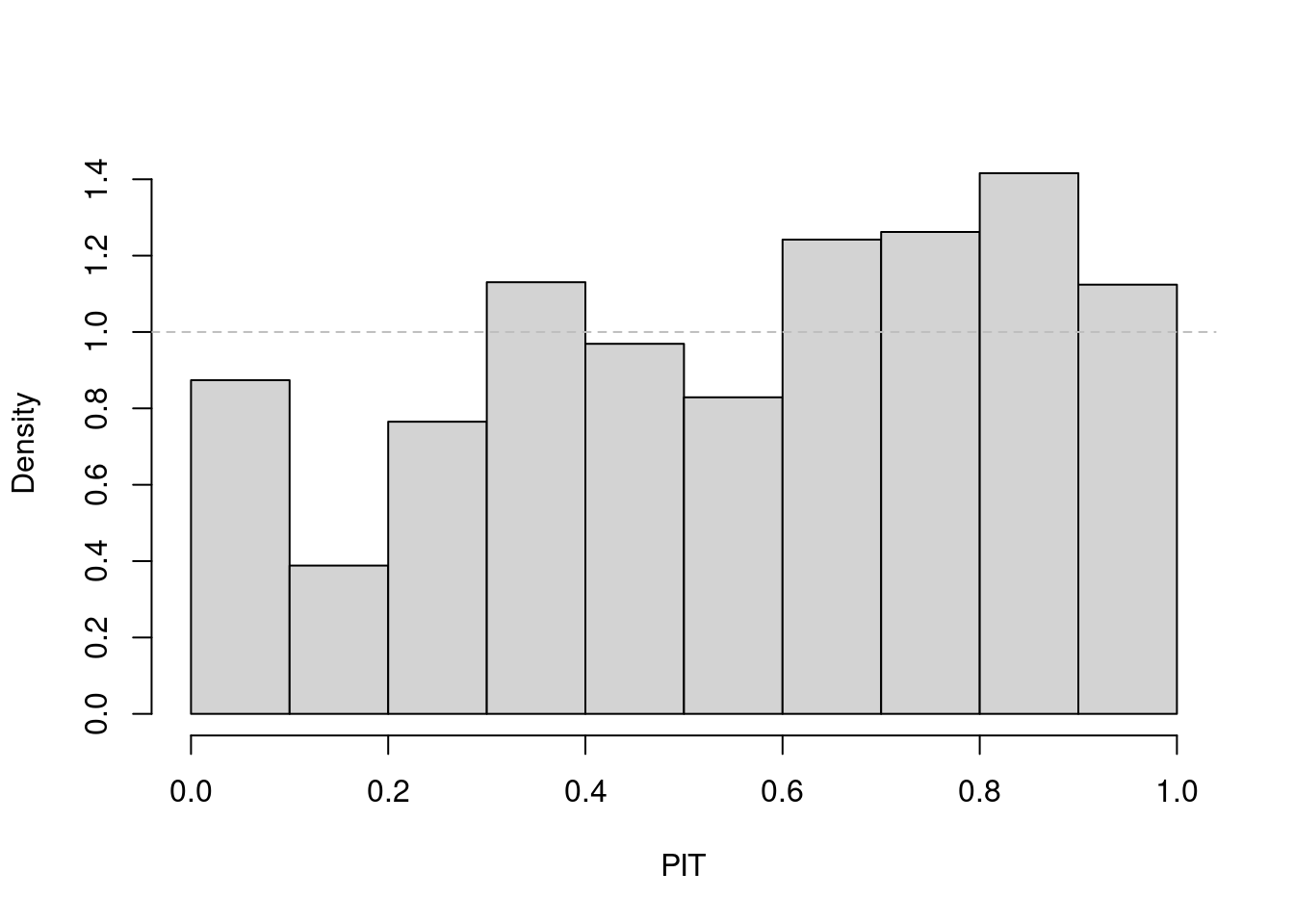
pit(osa01) # model tends to underpredict

## forecast from fit11 and compare mean scores() (where smaller is better)
osa11 <- oneStepAhead(fit11, startidx, verbose = FALSE)
rbind("constant lambda" = colMeans(scores(osa01)),
      "seasonal lambda" = colMeans(scores(osa11)))
                    logs      rps      dss      ses
constant lambda 4.169023 10.59943 6.514457 455.2519
seasonal lambda 4.167993 10.56779 6.517539 457.9010
## LS/RPS favour seasonal lambda, DSS favours constant lambda